Question

Find the length and foot of the perpendicular from the point $P\left( 7,14,5 \right)$ to the plane $2x+4y-z=2$.

Answer 1

Let us assume that the foot of the perpendicular on the plane is $Q\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$. Now, write the vector $\overrightarrow{PQ}$. Then write the vector normal to the given plane $2x+4y-z=2$. The vector normal to this plane is $2\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\,$and let name this vector as n. Now, the vector PQ is parallel to this vector n so apply the condition of two parallel vectors and then you get the value of ${{x}_{1}},{{y}_{1}},{{z}_{1}}$ in terms of some constant. Then to eliminate that constant satisfy the point Q in the equation of a plane $2x+4y-z=2$. Hence, you will get the point Q which is perpendicular. Now, to find the length of the perpendicular from point P to the plane find the distance between the point P and Q using distance formula.

Complete step by step answer:
We have given a plane with the following equation:
$2x+4y-z=2$
And we are asked to find the length and foot of the perpendicular from the point $P\left( 7,14,5 \right)$ to the plane.
Let us assume that the foot of the perpendicular from point $P\left( 7,14,5 \right)$ is $Q\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$. In the below diagram, we have shown a plane $2x+4y-z=2$ and points P and Q.

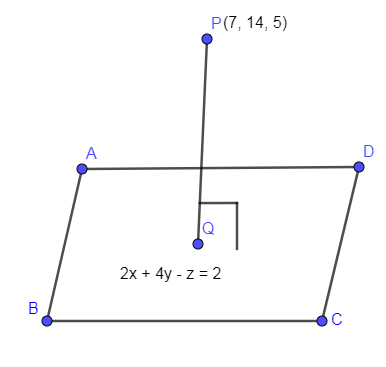
Now, the normal vector corresponding to the given plane $2x+4y-z=2$ is given as:
$2\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\,$
And we are denoting the vector by n so rewriting the above expression as:
$\overrightarrow{n}=2\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\,$
Now, find the vector PQ by subtracting x, y and z coordinate of point P from x, y and z coordinate of Q and multiplying the x coordinate, y coordinate and z coordinate difference by $\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\,$ respectively.
$\overrightarrow{PQ}=\left( {{x}_{1}}-7 \right)\overset{\wedge }{\mathop{i}}\,+\left( {{y}_{1}}-14 \right)\overset{\wedge }{\mathop{j}}\,+\left( {{z}_{1}}-5 \right)\overset{\wedge }{\mathop{k}}\,$
Now, normal vector n and the above vector PQ is parallel so their x, y and z coordinates are proportional.
$\dfrac{\left( {{x}_{1}}-7 \right)}{2}=\dfrac{\left( {{y}_{1}}-14 \right)}{4}=\dfrac{\left( {{z}_{1}}-5 \right)}{-1}=\lambda$
Now, equating each fraction to $\lambda$ we get,
$\begin{aligned} & \dfrac{\left( {{x}_{1}}-7 \right)}{2}=\lambda ; \\\ & \dfrac{\left( {{y}_{1}}-14 \right)}{4}=\lambda ; \\\ & \dfrac{\left( {{z}_{1}}-5 \right)}{-1}=\lambda \\\ \end{aligned}$
Solving each of the above equation we get,
$\begin{aligned} & {{x}_{1}}-7=2\lambda \\\ & \Rightarrow {{x}_{1}}=2\lambda +7 \\\ & {{y}_{1}}-14=4\lambda \\\ & \Rightarrow {{y}_{1}}=4\lambda +14 \\\ & {{z}_{1}}-5=-\lambda \\\ & \Rightarrow {{z}_{1}}=-\lambda +5 \\\ \end{aligned}$
From the above calculation, we have got the values of ${{x}_{1}},{{y}_{1}}\And {{z}_{1}}$ as follows:
$\begin{aligned} & {{x}_{1}}=2\lambda +7; \\\ & {{y}_{1}}=4\lambda +14; \\\ & {{z}_{1}}=-\lambda +5 \\\ \end{aligned}$
Now, the point Q lies on the plane so it will satisfy the equation of a plane. Substituting the coordinates of point Q in the equation of a plane we get,
$\begin{aligned} & 2x+4y-z=2 \\\ & \Rightarrow 2\left( 2\lambda +7 \right)+4\left( 4\lambda +14 \right)-\left( -\lambda +5 \right)=2 \\\ & \Rightarrow 4\lambda +14+16\lambda +56+\lambda -5=2 \\\ & \Rightarrow 21\lambda +65=2 \\\ \end{aligned}$
Subtracting 65 on both the sides of the above equation we get,
$\begin{aligned} & 21\lambda =2-65 \\\ & \Rightarrow 21\lambda =-63 \\\ & \Rightarrow \lambda =-\dfrac{63}{21}=-3 \\\ \end{aligned}$
Now, substituting the value of $\lambda$ in the coordinates of Q we get,
$\begin{aligned} & {{x}_{1}}=2\lambda +7 \\\ & \Rightarrow {{x}_{1}}=2\left( -3 \right)+7=-6+7=1 \\\ & {{y}_{1}}=4\lambda +14 \\\ & \Rightarrow {{y}_{1}}=4\left( -3 \right)+14=-12+14=2 \\\ & {{z}_{1}}=-\lambda +5 \\\ & \Rightarrow {{z}_{1}}=3+5=8 \\\ \end{aligned}$
Hence, the coordinates of Q are:
$\begin{aligned} & {{x}_{1}}=1; \\\ & {{y}_{1}}=2; \\\ & {{z}_{1}}=8 \\\ \end{aligned}$
Hence, the foot of the perpendicular (Q) is equal to $\left( 1,2,8 \right)$.
Now, to find the length of the perpendicular, we are going to find the distance between P and Q by distance formula.
Let us suppose that we have two points $Y\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\And Z\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ then using distance formula, the distance between these points is equal to:
$YZ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$
Now, using this distance formula in finding the distance between $P\left( 7,14,5 \right)\And Q\left( 1,2,8 \right)$ we get,
$\begin{aligned} & PQ=\sqrt{{{\left( 1-7 \right)}^{2}}+{{\left( 2-14 \right)}^{2}}+{{\left( 8-5 \right)}^{2}}} \\\ & \Rightarrow PQ=\sqrt{{{\left( -6 \right)}^{2}}+{{\left( -12 \right)}^{2}}+{{\left( 3 \right)}^{2}}} \\\ & \Rightarrow PQ=\sqrt{36+144+9} \\\ & \Rightarrow PQ=\sqrt{189} \\\ \end{aligned}$

Hence, the length of the perpendicular from point P to the plane is equal to $\sqrt{189}$.

Note: You can check the foot of perpendicular by substituting the point Q in the equation of a plane because the foot of perpendicular lies in the plane.
Point Q that we have found above is equal to $\left( 1,2,8 \right)$. Now, substituting this point in equation of a plane $2x+4y-z=2$ we get,
$\begin{aligned} & 2\left( 1 \right)+4\left( 2 \right)-8=2 \\\ & \Rightarrow 2+8-8=2 \\\ & \Rightarrow 2+0=2 \\\ & \Rightarrow 2=2 \\\ \end{aligned}$
As you can see that L.H.S = R.H.S of the above equation so the point Q is satisfying the equation of a plane.
Hence, the point Q that we have found out is correct.