Question

Find the length and foot of the ${{\bot }^{r}}$ from the point $P(7,14,5)$ to the plane $2x+4y-z=2$. Also find the image of the point P in the plane.

Answer 1

To solve the question, at first we have to consider the coordinate of the foot of the ${{\bot }^{r}}$ of P to the given plane to be $A({{x}_{1}},{{y}_{1}},{{z}_{1}})$. Then we must find out the vector and normal vector $\overrightarrow{N}$ to the plane from P. As $\overrightarrow{AP}$ and $\overrightarrow{N}$ are parallel to each other, then the ratios between corresponding x, y, and z components of two vectors must be equal to each other. By assuming each ratio to be equal to k and solving we can get the coordinate of the foot of the perpendicular from P. By using the distance formula we can obtain the length of the perpendicular from P to A. To find out image point we must consider the image point to be $B({{x}_{2}},{{y}_{2}},{{z}_{2}})$. By using the midpoint formula we get the midpoint of the line joining PB. Finally, by equating the coordinate of obtained midpoint with the coordinate of A, we will get the value of ${{x}_{2}},{{y}_{2}},{{z}_{2}}$.

Complete step-by-step solution:
__
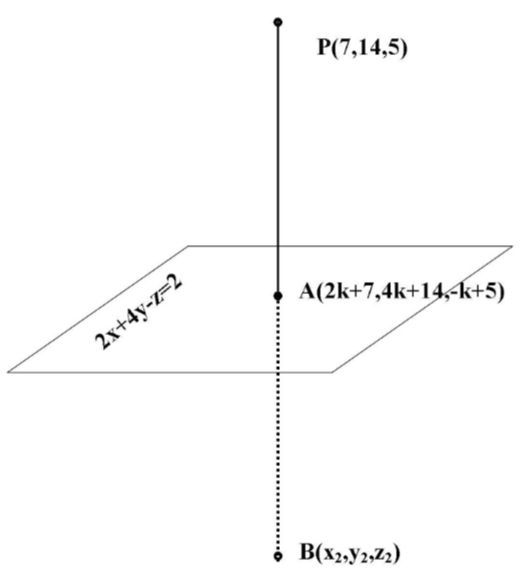
Consider the foot of the perpendicular from the point $P(7,14,5)$ to the plane $2x+4y-z=2$ is $A({{x}_{1}},{{y}_{1}},{{z}_{1}})$.
We know that vector from a point $(A,B,C)$ to a point $\left( a,b,c \right)$ is given by $\left( A-a \right)\hat{i}+(B-b)\hat{j}+(C-c)\hat{k}$.
Therefore the vector from $A({{x}_{1}},{{y}_{1}},{{z}_{1}})$ to $P(7,14,5)$ is given by
$\overrightarrow{AP}=\left( {{x}_{1}}-7 \right)\hat{i}+\left( {{y}_{1}}-14 \right)\hat{j}+({{z}_{1}}-5)\hat{k}$ …………………. (1)
We know the normal vector of a plane ${{a}_{1}}x+{{a}_{2}}y+{{a}_{3}}z=c$ is given by
${{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k}$.
Hence the vector of a plane $2x+4y-z=2$ is given by
$\vec{N}=2\hat{i}+4\hat{j}-\hat{k}$ ……………………. (2)
As both of $\overrightarrow{AP}$ and $\overrightarrow{N}$ are perpendicular to the same plane, then $\overrightarrow{AP}\parallel \vec{N}$ and the ratios of respective x, y and z components of the vectors must be equal to each other. Hence
$\dfrac{\left( {{x}_{1}}-7 \right)}{2}=\dfrac{\left( {{y}_{1}}-14 \right)}{4}=\dfrac{({{z}_{1}}-5)}{-1}$
Consider $\dfrac{\left( {{x}_{1}}-7 \right)}{2}=\dfrac{\left( {{y}_{1}}-14 \right)}{4}=\dfrac{({{z}_{1}}-5)}{-1}=k$
$\Rightarrow {{x}_{1}}=2k+7,{{y}_{1}}=4k+14,{{z}_{1}}=-k+5$ …………………………… (3)
Hence the coordinate of the foot of the perpendicular is given by $A\left( 2k+7,4k+14,-k+5 \right)$. Since the foot of the perpendicular lies on the plane $2x+4y-z=2$, then the coordinate of the foot must satisfy the plane equation. Thus substituting the x, y and z coordinates of the point in place of x, y and z in the plane equation, we will get,

& \Rightarrow 2(2k+7)+4(4k+14)-(-k+5)=2 \\\ & \Rightarrow 4k+14+16k+56+k-5=2 \\\ & \Rightarrow 21k+65=2 \\\ & \Rightarrow 21k=-63 \\\ \end{aligned}$$ $$\Rightarrow k=-3$$……………………………… (4) Now the coordinate of A is $$\left( 2(-3)+7,4(-3)+14,-(-3)+5 \right)$$ that equals to $$(1,2,8)$$. The length of the perpendicular AP is the distance between the points $$A(1,2,8)$$ and $$P(7,14,5)$$ which is given by $$\begin{aligned} & AP=\sqrt{{{(7-1)}^{2}}+{{(14-2)}^{2}}+{{(5-8)}^{2}}} \\\ & =\sqrt{{{6}^{2}}+{{12}^{2}}+{{(-3)}^{2}}} \\\ & =\sqrt{189} \\\ & =3\sqrt{21} \end{aligned}$$ Consider the image point of $$P(7,14,5)$$ be $$B({{x}_{2}},{{y}_{2}},{{z}_{2}})$$ in the plane. We know the formula that midpoint of the line joining $$\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$$ and $$\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$$ are given by $$\left( \dfrac{{{a}_{1}}+{{a}_{2}}}{2},\dfrac{{{b}_{1}}+{{b}_{2}}}{2},\dfrac{{{c}_{1}}+{{c}_{2}}}{2} \right)$$ Hence applying the formula that midpoint of the line joining $$P(7,14,5)$$and$$B({{x}_{2}},{{y}_{2}},{{z}_{2}})$$ is given by $$\left( \dfrac{7+{{x}_{2}}}{2},\dfrac{14+{{y}_{2}}}{2},\dfrac{5+{{z}_{2}}}{2} \right)$$. But here formula that midpoint of the line joining $$P(7,14,5)$$and$$B({{x}_{2}},{{y}_{2}},{{z}_{2}})$$ must be $$A(1,2,8)$$ since it is the foot of the perpendicular from P on the plane and $$PA=AB$$. Therefore we can obtain the values of $${{x}_{2}},{{y}_{2}},{{z}_{2}}$$ by equating the respective coordinates of $$\left( \dfrac{7+{{x}_{2}}}{2},\dfrac{14+{{y}_{2}}}{2},\dfrac{5+{{z}_{2}}}{2} \right)$$ and $$(1,2,8)$$. Here we will get $$\begin{aligned} & \Rightarrow \dfrac{7+{{x}_{2}}}{2}=1,\dfrac{14+{{y}_{2}}}{2}=2,\dfrac{5+{{z}_{2}}}{2}=8 \\\ & \Rightarrow {{x}_{2}}=-5,{{y}_{2}}=-10,{{z}_{2}}=11 \end{aligned}$$ **The image of $$P(7,14,5)$$ in the plane is $$B(-5,-10,11)$$.** **Note:** Always remember that the distance between the points joining $$\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$$ and $$\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$$ is given by $$\sqrt{{{({{a}_{2}}-{{a}_{1}})}^{2}}+{{({{b}_{2}}-{{b}_{1}})}^{2}}+{{({{c}_{2}}-{{c}_{1}})}^{2}}}$$ and if a point having coordinate $$({{x}_{1}},{{y}_{1}},{{z}_{1}})$$ satisfies an equation $$f(x,y,z)=0$$ then $$f({{x}_{1}},{{y}_{1}},{{z}_{1}})=0$$ that means the x, y and z coordinates of the point replaces x, y and z respectively in the equation. Draw figure according to data given in question, as it will help in solving the question more easily and accurately. Try not to make any calculation mistake as this will change the final answer of the solution.