Question

Find the left hand limit and right hand limit of the function$f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x = 2$

Answer 1

Define the function for the values of $x < 2$and$x > 2$. Compute their limits using the properties of absolute value and the fact that the limit of a constant function is the constant.
These limits will be the required answer.

Complete step by step answer:
Finding the left hand and right hand limits of a function$f(x)$at a point$x = a$means finding the limit of $f(x)$ at $x < a$and finding the limit of $f(x)$ at $x > a$respectively where $a$ is any real number.
The left hand limit of $f(x)$ at $x < a$ is denoted by$\mathop {\lim }\limits_{x \to {a^ - }} f(x)$ if it exists.
Similarly, the right hand limit of$f(x)$ at $x > a$is denoted by $\mathop {\lim }\limits_{x \to {a^ + }} f(x)$ if it exists.
Therefore, to find the left and right hand limits we need to define the value of$f(x)$ at $x > a$and at $x < a$ respectively.
In the given question, we have
$a = 2$ and $f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x = 2$
Therefore, we will determine the value of $f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x < 2$ and $x > 2$
Let’s recall the behaviour of the absolute value function.
For a real number $x$
If $x < 0$, then $|x| = - x$ and
if $x > 0$, then $|x| = x$
Consider the graph of the absolute value function.

Thus, when $x < 2$,

$$x - 2 < 0 \\\ \Rightarrow |x - 2| = - (x - 2) \\\$$

Therefore, $f(x) = \dfrac{{|x - 2|}}{{x - 2}} = \dfrac{{ - (x - 2)}}{{x - 2}} = - 1$
Thus, $f(x)$ is a constant function when $x < 2$
We know that the limit of a constant function is equal to the constant.
This implies that $\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} ( - 1) = - 1$.
That is, the left hand limit of the given function $f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x = 2$ is $- 1$
Similarly, we need to find the right hand limit of $f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x = 2$
Now, when $x > 2$

$$x - 2 > 0 \\\ \Rightarrow |x - 2| = x - 2 \\\$$

Therefore, we have $f(x) = \dfrac{{|x - 2|}}{{x - 2}} = \dfrac{{x - 2}}{{x - 2}} = 1$
Below is the graph of the function$f(x) = \dfrac{{|x - 2|}}{{x - 2}}$

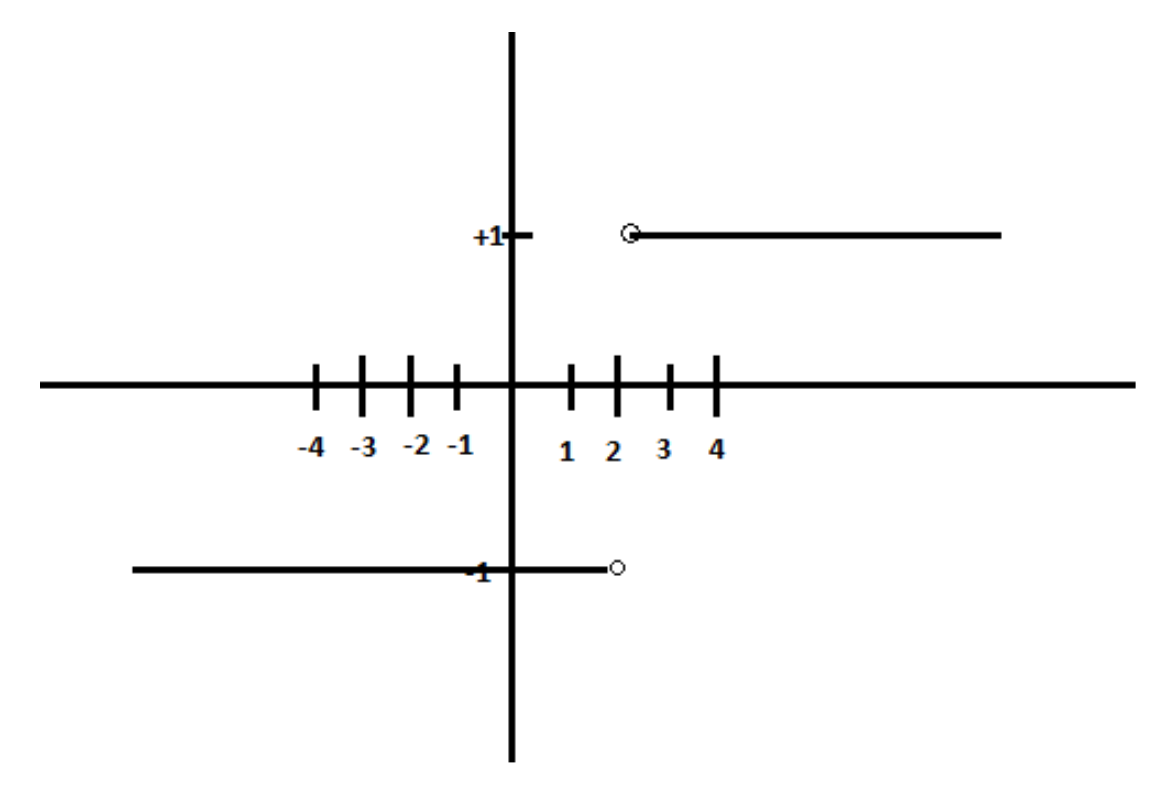
Thus, $f(x)$ is a constant function when $x > 2$ as well.
Let us compute the right hand limit of $f(x)$.
$\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} (1) = 1$.
Thus, the right hand limit of the given function is 1.
Hence the left hand and right hand limits of the function $f(x) = \dfrac{{|x - 2|}}{{x - 2}}$ at $x = 2$ are $- 1$ and $1$ respectively.

Note: It is advisable to draw a graph of a function to understand the nature of the function for which the left hand and right hand limits are to be calculated. Functions are best understood with the help of graphs.