Question

Find the least pulling force which, acting at an angle of ${{45}^{\circ }}$ with horizontal, will slide a body weighing 5kg along a rough horizontal surface. The coefficient of friction ${{\mu }_{S}}={{\mu }_{K}}=1/3$. If force of double this applied along the same direction, find the resulting acceleration of the block

Answer 1

To solve the above question we will first resolve the above force into vertical and horizontal components. Further we will determine the normal force acting on the block with respect to the mass of the body and the vertical component of P. The least value of P will be obtained when the horizontal component of P overcomes the frictional force. Further we will do the same when the value of the Force P is doubled.

Formula used:
$N=mg-PSin{{45}^{\circ }}$
$\begin{aligned} & F(static friction)={{\mu }_{S}}N \\\ & F(kinetic friction)={{\mu }_{K}}N \\\ \end{aligned}$
$F=ma$

Complete answer:
To begin with let us draw the free body diagram of the above block of mass m. Further lets express pulling force P in terms of its vertical and horizontal components.

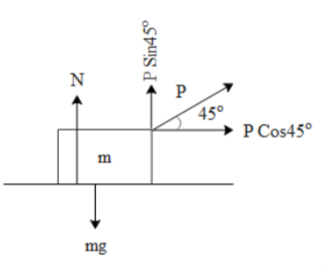
There is no vertical motion of the block. Hence we can say that the net force on the block along the vertical is zero. In the above free body diagram we can see that the Normal force (N) on the block of mass ‘m’ can be written as,
$N=mg-PSin{{45}^{\circ }}$
The block will not move till the horizontal component of P i.e. $PCos{{45}^{\circ }}$ overcomes the force of friction. The force of friction for a body at rest is given by the product of the Normal times the coefficient of static friction. Mathematically, this can be represented as,
$F(static friction)={{\mu }_{S}}N$
Hence for the block to move, the minimum pulling force is equal to,
$\begin{aligned} & PCos{{45}^{\circ }}=F(friction) \\\ & \Rightarrow PCos{{45}^{\circ }}={{\mu }_{S}}N\text{, }\because N=mg-PSin{{45}^{\circ }}and{{\mu }_{S}}=1/3 \\\ & \Rightarrow PCos{{45}^{\circ }}=\dfrac{mg-PSin{{45}^{\circ }}}{3} \\\ & \Rightarrow PCos{{45}^{\circ }}+\dfrac{PSin{{45}^{\circ }}}{3}=\dfrac{5\times 10}{3} \\\ & \Rightarrow P(Cos{{45}^{\circ }}+\dfrac{Sin{{45}^{\circ }}}{3})=\dfrac{50}{3} \\\ & \Rightarrow P=\dfrac{50}{3(Cos{{45}^{\circ }}+\dfrac{Sin{{45}^{\circ }}}{3})}=\dfrac{50}{3(\dfrac{3Cos{{45}^{\circ }}+Sin{{45}^{\circ }}}{3})} \\\ & \Rightarrow P=\dfrac{50}{3Cos{{45}^{\circ }}+Sin{{45}^{\circ }}}\text{, }Cos{{45}^{\circ }}=Sin{{45}^{\circ }}=\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow P=\dfrac{50}{\dfrac{3+1}{\sqrt{2}}}=\dfrac{50\sqrt{2}}{4}=\dfrac{25}{\sqrt{2}}N \\\ \end{aligned}$
If a force of 2P is applied to the block, it is given to us that the block will move with net acceleration ‘a’. When the block starts due to action of force 2P, the force of friction is given by,
$F(kinetic friction)={{\mu }_{K}}N$ where is equal to $N=mg-2PSin{{45}^{\circ }}$. Hence the net force F on the block when force applied is 2P is given by,
$F=2PCos{{45}^{\circ }}-F(kinetic friction)$
Since from Newton’s second law, force is defined as mass times the acceleration i.e. $F=ma$, the above equation becomes,
$\begin{aligned} & ma=2PCos{{45}^{\circ }}-F(kinetic friction) \\\ & \Rightarrow ma=2PCos{{45}^{\circ }}-{{\mu }_{K}}(mg-2PSin{{45}^{\circ }}) \\\ & \Rightarrow 5kga=2\dfrac{25}{{{\left( \sqrt{2} \right)}^{2}}}-\left( \dfrac{5\times 10-2\times \dfrac{25}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}}}{3} \right) \\\ & \Rightarrow 5kga=2\dfrac{25}{2}-(\dfrac{5\times 10-2\times \dfrac{25}{2}}{3}) \\\ & \Rightarrow 5kga=25-(\dfrac{50-25}{3}) \\\ & \Rightarrow 5kga=\dfrac{75-25}{3}=\dfrac{10}{3}m{{s}^{-2}} \\\ & \Rightarrow a=\dfrac{25}{3}m{{s}^{-2}} \\\ \end{aligned}$

Note:
It is to be noted that the frictional force always opposes the motion of the body. hence we have taken it to be opposite to the motion of the body. The difference between the coefficient of static friction and coefficient of kinetic friction is that the frictional coefficient of the surface is usually different when the body is in motion and at rest.