Question

Find the least number which is divided by 5, 6, 8, 9, 12 leaves a remainder 1 but when divided by 13 leaves no remainder.
A.3601
B.1469
C.2091
D.4879

Answer 1

Here, we will first find the LCM of 5, 6, 8, 9 and 12. We will assume that the required number is 1 greater than a multiple of the LCM. Then we will find the required number using Euclid’s Division Lemma.

Formulas used:
We will use the formula of Euclid’s Division lemma which is given by $a = bq + r$.

Complete step-by-step answer:
Let the required number be $x$. We know that when $x$ is divided by 13, it does not leave any remainder. This means that $x$ is divisible by 13.
Any number that leaves a remainder of 1 on being divided by 5, 6, 8, 9 and 12 will also leave a remainder of 1 on being divided by the LCM of 5, 6, 8, 9 and 12. We will find the L.C.M. of 5, 6, 8, 9 and 12:

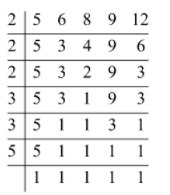
Now, the L.C.M. is given by:
$\begin{array}{l}{\rm{LCM}} = 2 \times 2 \times 2 \times 3 \times 3 \times 5\\\\{\rm{LCM}} = 360\end{array}$
As the number will leave a remainder 1 on being divided by 360, we will substitute 1 for $r$, $x$ for $a$ and 360 for $b$ in Euclid’s division lemma, $a = bq + r$. Therefore, we get
$x = 360q + 1$……………………$\left( 1 \right)$
We will substitute different values for $q$ in the above equation and check whether the $x$ we obtain is divisible by 13. We will do this till we find a number divisible by 13. This method is called the method of trial and error.
Substituting 1 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360 + 1\\\ \Rightarrow x = 361\end{array}$
361 is not divisible by 13.
Substituting 2 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 2 \right) + 1\\\ \Rightarrow x = 721\end{array}$
721 is not divisible by 13.
Substituting 3 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 3 \right) + 1\\\ \Rightarrow x = 1081\end{array}$
1081 is not divisible by 13.
Substituting 4 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 4 \right) + 1\\\ \Rightarrow x = 1441\end{array}$
1441 is not divisible by 13.
Substituting 5 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 5 \right) + 1\\\ \Rightarrow x = 1801\end{array}$
1801 is not divisible by 13.
Substituting 6 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 6 \right) + 1\\\ \Rightarrow x = 2161\end{array}$
2161 is not divisible by 13.
Substituting 7 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 7 \right) + 1\\\ \Rightarrow x = 2521\end{array}$
2521 is not divisible by 13.
Substituting 8 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 8 \right) + 1\\\ \Rightarrow x = 2881\end{array}$
2881 is not divisible by 13.
Substituting 9 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( 9 \right) + 1\\\ \Rightarrow x = 3241\end{array}$
3241 is not divisible by 13.
Substituting 10 for $q$ in equation $\left( 1 \right)$, we get
$\begin{array}{l}x = 360\left( {10} \right) + 1\\\ \Rightarrow x = 3601\end{array}$
3601 is divisible by 13.
$\therefore$ The least number which is divided by 5, 6, 8, 9, 12 leaves a remainder 1 but when divided by 13 leaves no remainder is 3601.
Option A is the correct option.

Note: The above method is a lengthy and tedious method. We can also find the answer by choosing the least number from the options and checking whether it is divisible by 13 and leaves a remainder of 1 on being divided by 360. Option B is divisible by 13 but doesn’t leave a remainder of 1 on being divided by 360. Option C is not divisible by 13. Option fulfils both the criteria, so it’s the correct option.
If a number (say $a$) on being divided by another number (say b) leaves a remainder $r$ and has a divisor $q$, then according to Euclid’s Division lemma: $a = bq + r$
where $0 \le r < b$ and $a$ and $b$ are integers.