Question

Find the inverse of a point a with respect to the circle $|z-c|=R$(a and c are complex numbers, centre C and radius R).

Answer 1

Now we know that inverse a center and the point lies on the same line. Hence we get the condition $\arg (a'-c)=\arg (a-c)$ . Now we will use properties of argument $\arg (\bar{z})=-\arg (z)$ and $\arg ({{z}_{1}}{{z}_{2}})=\arg \left( {{z}_{1}} \right)+\arg \left( {{z}_{2}} \right)$ to prove that $\left( a'-c \right)(\bar{a}-\bar{c})$ then we will use the facts that if a is real then $|a|=a$. Now since a and a’ lies on circle we know that $|a'-c|=|a-c|=R$. Using this we will find the equation in a, a’, c and R.

Complete step by step answer:
Now we need to find inverse of a point a with respect to the circle $|z-c|=R$ to do so let us consider the inverse point as a’.

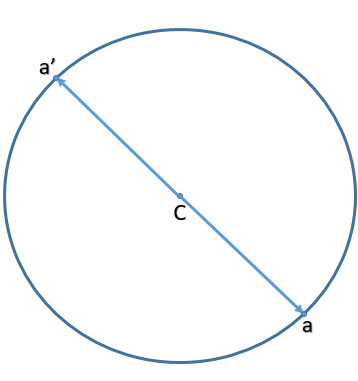
Now we have a’ be inverse of a with respect to the circle $|z-c|=R$
Now we know that a, c, a’ are all collinear points
Hence we get
$\arg (a'-c)=\arg (a-c)$
Now we know that $\arg (\bar{z})=-\arg (z)$, using this result we get
$\arg (a'-c)=-\arg (\bar{a}-\bar{c})$
Taking $\arg (\bar{a}-\bar{c})$ to LHS we get
$\arg (a'-c)+\arg (\bar{a}-\bar{c})=0$
Now we also know that $\arg ({{z}_{1}}{{z}_{2}})=\arg \left( {{z}_{1}} \right)+\arg \left( {{z}_{2}} \right)$ , using this result we get
$\arg [\left( a'-c \right)(\bar{a}-\bar{c})]=0$
Now if we have $\arg \left( z \right)=0$ this means that z lies on real axis and hence z is real
Hence we can say that $\arg [\left( a'-c \right)(\bar{a}-\bar{c})]=0$ which means that $\left( a'-c \right)(\bar{a}-\bar{c})$ is real…………… (1)
Now we know that the point a and a’ lies on circle with radius R, hence we can say
$|a-c|=R$ and $|a'-c|=R$
Hence we have $|a-c||a'-c|={{R}^{2}}$
Now we have $|\bar{z}|=|z|$ , using this we can write $|a-c|=|\bar{a}-\bar{c}|$
Hence we get,
$|\bar{a}-\bar{c}||a'-c|={{R}^{2}}$
$\Rightarrow |\left( \bar{a}-\bar{c} \right)\left( a'-c \right)|={{R}^{2}}$
But from (1) we know that $\left( a'-c \right)(\bar{a}-\bar{c})$ is real
Now if a is real then $|a|=a$
Hence we get

& \left( \bar{a}-\bar{c} \right)\left( a'-c \right)={{R}^{2}} \\\ & \Rightarrow (a'-c)=\dfrac{{{R}^{2}}}{\left( \bar{a}-\bar{c} \right)} \\\ & \Rightarrow a'=c+\dfrac{{{R}^{2}}}{\left( \bar{a}-\bar{c} \right)} \\\ \end{aligned}$$ **Hence now we have inverse of a that is a’ is such that $$a'=c+\dfrac{{{R}^{2}}}{\left( \bar{a}-\bar{c} \right)}$$** **Note:** Note that $|x+iy|=\sqrt{{{x}^{2}}+{{y}^{2}}}$ hence if y = 0 we get |x|=x. hence this is only true if the complex number is purely real. Hence if we use |a| = a, we first need to prove that a is real.