Question

Find the interval in which the smallest positive of the equation $\tan x-x=0$ lies
(a) $\left( 0,\dfrac{\pi }{2} \right)$
(b) $\left( \dfrac{\pi }{2},\pi \right)$
(c) $\left( \pi ,\dfrac{3\pi }{2} \right)$
(d) $\left( \dfrac{3\pi }{2},2\pi \right)$

Answer 1

Hint: Roots of any equation $f\left( x \right)=g\left( x \right)$ or $f\left( x \right)-g\left( x \right)=0$ can be calculated by drawing the curves of both $f\left( x \right)$ and $g\left( x \right)$ and get the intersection points which will be the roots of equations. Verify that $y=x$ will touch $\tan x$ or not. Tangent equation for any curve $f\left( x \right)$ at $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as
$y-{{y}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)$

Complete step-by-step solution -
As, we know the solution or roots of any equation $f\left( x \right)=g\left( x \right)$ or $f\left( x \right)-g\left( x \right)=0$will be given by drawing the graphs of $f\left( x \right)$ and $g\left( x \right)$ and the value of $x$ at which $f\left( x \right)$ will be equal to $g\left( x \right)$ will be a solution of the given equation i.e. the intersection points of $f\left( x \right)$ and $g\left( x \right)$ will give the roots of the equation $f\left( x \right)=g\left( x \right)$
Now, coming to the question as we need to determine the smallest positive root of the equation $\tan x - x=0$ or . So, let us draw the graph of $y=\tan x$ and $y=x$ and get the intersection points, which will determine the roots of the equation $\tan x=x$ and hence, we can get the least positive value of $x,$ which satisfy the equation $\tan x=x$
As we know curve $y=x$ can be given as

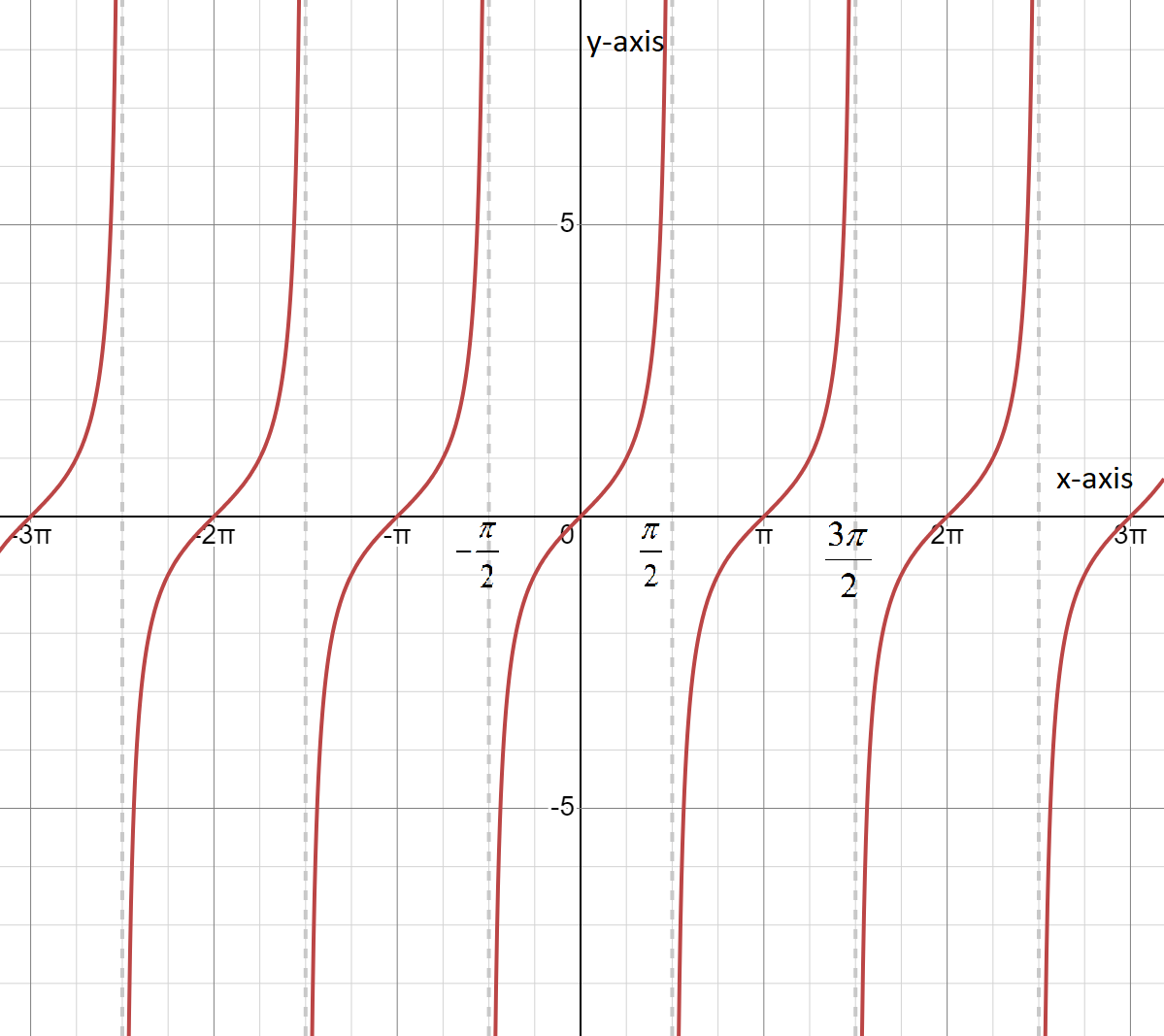
And curve $y=\tan x$ can be given as

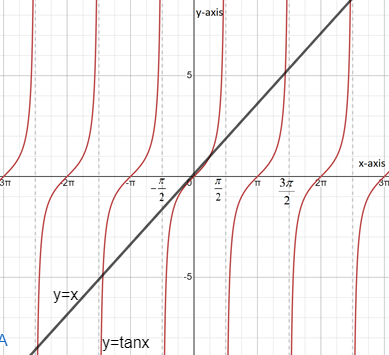
As we know, we have to calculate the range of the first positive root of the equation $\tan x=x$ .So, Let us draw curves of $y=\tan x$ and $y=x$ in the same coordinate plane. So, we get

Now, let us calculate the equation of tangent for curve $y=\tan x$ at (0,0)
As we know equation of a tangent for any curve $f\left( x \right)$ at $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as
$y-{{y}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)..........\left( i \right)$
So $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as (0,0). Let us calculate value of $\dfrac{dy}{dx}$ by following way:
We have
$y=\tan x$
Differentiating the equation w.r.t. $x$ we get
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left( \tan x \right)$
We know $\dfrac{d}{d\theta }={{\sec }^{2}}\theta$
Hence, we get $\dfrac{dy}{dx}={{\sec }^{2}}x$
So, we get
${{\left. \dfrac{dy}{dx} \right|}_{\left( 0,0 \right)}}={{\sec }^{2}}0={{1}^{2}}=1$
Hence, slope of the tangent i.e. ${{\left. \dfrac{dy}{dx} \right|}_{\left( 0,0 \right)}}=1$ . Hence equation of tangent to the curve $y=\tan x$ at (0,0) is given as
$\begin{aligned} & y-0=1\left( x-0 \right) \\\ & y=x.......\left( ii \right) \\\ \end{aligned}$
Now, we get that $y=x$ is acting as a tangent to the curve $y=\tan x$ at (0,0). It means curve $y=\tan x$ will not meet the curve $y=\tan x$ between $-\dfrac{\pi }{2}$ and $\dfrac{\pi }{2}$ at anywhere else other (0, 0).
So, we can easily observe that $y=x$ will intersect $y=\tan x$ between $x=\pi$ to $x=\dfrac{3\pi }{2}$ , as value of $y=\tan x$ will be negative from $x=\dfrac{\pi }{2}$ to $x=\pi$ .So, the exact interval for the first positive root of the equation $\tan x=x$ will be given as $\left( \pi ,\dfrac{3\pi }{2} \right)$
So, option(c) is the correct answer.

Note: $x=0$ is not a positive root of the equation $\tan x=x$ as 0 is not considered as a positive number, it comes under non-negative integers. So, don’t confuse with this point in the solution. One may go wrong if/she does not check for the tangent equation of $y=\tan x$ at (0,0), one may answer the questions as $\left( 0,\dfrac{\pi }{2} \right)$ if he/she intersect the equation $y=x$ and $y=\tan x$ in between 0 to $\dfrac{\pi }{2}$ , which is wrong as $y=x$ is acting as a tangent for $y=\tan x$ at (0,0). So, be careful with this part of the solution.