Question

Find the interval in which the function given by $f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\$ is
A. Strictly increasing
B. Strictly decreasing

Answer 1

In this question, we need to find the interval of the given expression $f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\$ and need to conclude that the interval of the expression is increasing or decreasing. First, we need to find the differentiation of $f(x)$ that is $f’(x)$. Then we check $f’(x) = 0$ . Using this we can find the value of $x$ and then we need to plot the value of $x$ in a number , in order to find the interval of $f(x)$ .

Complete answer:
Given,
$f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11$
First let us differentiate the given expression $f(x)$ .
That is $f’\left( x \right) = \dfrac{3}{10}\left( 4x^{3} \right) - \dfrac{4}{5}\left( 3x^{2} \right) – 3\left( 2x \right) + \dfrac{36}{5} + 0$
On simplifying,
We get ,
$\Rightarrow \ f^{‘}\left( x \right) = \dfrac{6}{5}x^{3} - \dfrac{12}{5}x^{2} – 6x + \dfrac{36}{5}$
Now on taking LCM,
We get
$\Rightarrow \ f’(x) = \left( \dfrac{6x^{3} – 12x^{2} – 30x + 36}{5} \right)$
On taking 6 common,
We get ,
$\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – 2x^{2} – 5x + 6 \right)$
Now on splitting the terms in parentheses,
We get
$\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – x^{2} – x^{2} + x – 6x + 6 \right)$
Now on taking $(x – 1)$ common,
We get,
$\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{2}\left( x – 1 \right) – x\left( x – 1 \right) – 6\left( x – 1 \right) \right)$
Thus we get,
$\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x^{2} – x – 6 \right) \right)$
Again on factoring the term $\left( x^{2} – x – 6 \right)$
We get,
$\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right)$
On putting $f’(x)\ = 0$ ,
We get,
$\dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0$
Now on multiplying both sides by $\dfrac{5}{6}$,
We get,
$\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0$
Here $x = 1,\ - 2,\ 3$
Now let us point the values of $x$ in a number line.

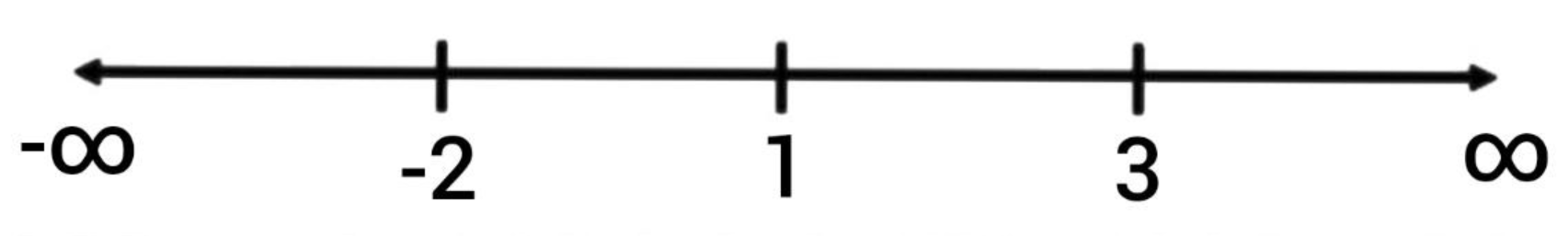
Values of $x$	Intervals	Sign of $f’(x) = 0$	Nature of $f(x)$
$- \infty < x < \- 2$	$( - \infty,\ - 2)$	$( - )( - )( - )\ < 0$	Strictly decreasing
$- 2 < x < 1$	$( - 2,\ 1)$	$( - )( + )( - ) > 0$	Strictly increasing
$1 < x < 3$	$(1,\ 3)$	$( + )( + )( - )\ < 0$	Strictly decreasing
$3 < x < \infty$	$(3,\ \infty)$	$( + )( + )( + ) > 0$	Strictly increasing

Hence $f(x)$ is strictly increasing in the interval $( - 2,\ 1)$ and $(3,\ \infty)$
And $f(x)$ is strictly decreasing in the interval of $( - \infty,\ - 2)$ and $(1,\ 3)$
Final answer :
A. $f(x)$ is strictly increasing in the interval $( - 2,\ 1)$ and $(3,\ \infty)$
B. $f(x)$ is strictly decreasing in the interval of $( - \infty,\ - 2)$ and $(1,\ 3)$

Note: In order to solve these types of questions, we should have a strong grip over strictly increasing and decreasing functions. We also need to know that a function is said to increase when the y-value increases as the x-value increases similarly, a function is said to be decreasing when the x-value increases as the y-value increases. We should be very careful , while splitting the intervals of the function.