Question

Find the integral of $\cos 2x$.

Answer 1

Integration is a way of adding slices to find the whole.
Integration can be used to find areas, volumes, central points and many useful things.
But it is easiest to start with finding the area under the curve of a function like this

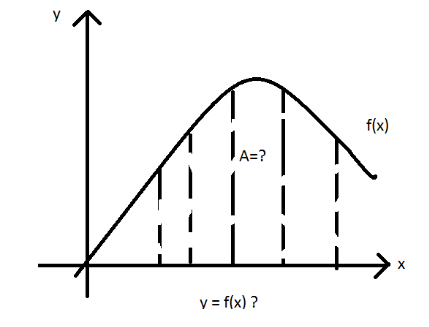
$y = f(x)?$
The symbol for ‘integral’ is $'\int '$.
For example
$\int {2x\,dx}$
After the integral symbol we put the function we want to find the integral of and then finish with dx to mean the slice go in the x direction (and approach zero in width)
$\int {2x\,dx = {x^2}} + c$
Where ‘c’ is the ‘constant integration.’
Therefore,

Complete step-by-step answer:
To integrate cos2x, also written as $\sqrt {\cos 2x\,dx}$ and cos2x we usually use a ’u’ substitution to build a new integration in term of u

Let\,u = 2x \\\ \dfrac{{du}}{{dx}} = 2 \\\ \end{gathered} $$ Then $$\begin{gathered} du = 2 \\\ dx \\\ dx = \dfrac{1}{2}du \\\ \end{gathered} $$ We arrange to get and expression for ‘dx’ in terms of u Now, $$\int {\cos 2x\,dx = \int {\cos u\dfrac{1}{2}} du} $$ We get this by replacing 2x with u and replacing ‘dx’ will $${Y_2}$$du $$\int {\cos u\dfrac{1}{2}du} = \dfrac{1}{2}\int {\cos u\,du} $$ We move the $$\dfrac{1}{2}$$ outside of the integral as it is simply a multiplier. $$\int {\operatorname{Cos} u = \operatorname{Sin} u} $$ Now we have a simple integration with $$\operatorname{Sin} \,u$$ $$\dfrac{1}{2}\int {\cos \,u\,du = \dfrac{1}{2}\operatorname{Sin} \,u} $$ We remember the $$\dfrac{1}{2}$$ outside the integral sign and reintroduce it here $$ = \dfrac{1}{2}\operatorname{Sin} 2x + C$$ Hence, this is the final answer where C is the integration constant. **Note:** Finding an integral is the reverse of finding a derivative. In the differential we are given a function and we have to find the derivative or difference of the function, but in the integral, we are to find a function whose differential is given.