Question

Find the instantaneous axis of rotation of a rod of length l when its end A moves with velocity ${{v}_{\text{A}}}=v\widehat{i}$ and the rod rotates with angular velocity $\omega =-\dfrac{v}{2l}\widehat{k}$

Answer 1

To find the instantaneous axis of rotation of a rod of length l, we first need to locate the ICR i.e. the instantaneous centre of rotation. The velocity of this point is always relatively taken to be zero. Hence further expressing the different components of velocities at this point we will obtain the instantaneous axis of rotation of a rod of length l with respect to its end A.

Formula used:
$v=\omega r$

Complete step-by-step answer:
First let us take a point P as the ICR in the extended version of the rod. The relative velocity of this point is always zero. Given below is a figure to understand the location of ICR.

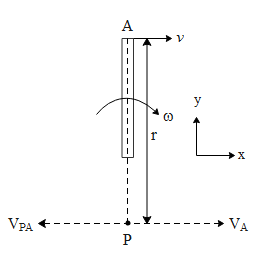
The velocity of the point P is zero. Hence from the above figure we can write
$\begin{aligned} & {{v}_{P}}={{v}_{PA}}+{{v}_{A}} \\\ & \because {{v}_{P}}=0 \\\ & \therefore {{v}_{PA}}+{{v}_{A}}=0.....(1) \\\ \end{aligned}$
The velocity with which the point P moves is equal to ${{v}_{\text{A}}}=v\widehat{i}$ and the velocity with which the point A moves with respect to P is ${{v}_{\text{PA}}}=\omega r\widehat{i}$ where ‘r’ is the distance of point P from point A.
Hence from equation 1 we obtain,
$\begin{aligned} & {{v}_{PA}}+{{v}_{A}}=0 \\\ & \Rightarrow \omega r\widehat{i}+v\widehat{i}=0 \\\ & \therefore v=\omega r \\\ \end{aligned}$
In the question it is given that the rod rotates with angular velocity equal to $\omega =-\dfrac{v}{2l}\widehat{k}$. Therefore from the above equation we obtain the position of the instantaneous axis of rotation with respect to A at,
$\begin{aligned} & v=\omega r \\\ & \Rightarrow v=-\dfrac{v}{2l}r \\\ & \therefore r=2l \\\ \end{aligned}$
Hence the instantaneous axis of rotation of a rod lies at 2l from end A of the rod.

Note: Instantaneous center of rotation (ICR) is an imaginary point about which a link is assumed to rotate. This point has certain properties which can be used to simplify the motion of the body. This point may lie or sometimes may not lie on the body.