Question

Find the inflection points and the intervals in which the function $f\left( x \right) = {x^4} - 4{x^3}$ is concave up and concave down.

Answer 1

Hint – In this particular types of questions use the concept that point of inflection is the intersection point of the given curve with the x-axis and in concave up the graph is upwards the x-axis and in concave down the graph is below the x-axis so use this concept to reach the solution of the question.

Complete step-by-step answer:

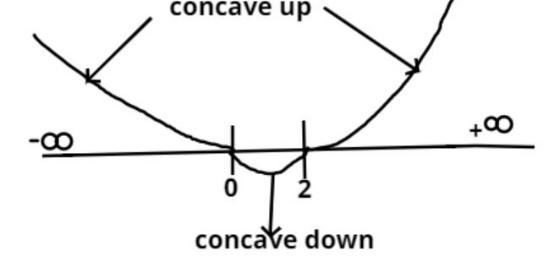
Point of inflection
Point of inflection is the intersection point of the curve with the x-axis, we calculate this point of inflection by double differentiating the given equation with respect to the x and equate to zero, then solve for x, so the evaluated value of x is the required point of inflection.
$\Rightarrow f''\left( x \right) = 0$
Concave up
To concave up the double differentiation of the function should be greater than zero.
I.e. $f''\left( x \right) > 0$
Concave down
To concave down the double differentiation of the function should be less than zero.
I.e. $f''\left( x \right) < 0$
Now the given curve is
$f\left( x \right) = {x^4} - 4{x^3}$.................. (1)
Now differentiate this curve using the property that $f'\left( x \right) = \dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}$ so we have,
So the differentiation of the equation (1) is given as
$\Rightarrow f'\left( x \right) = 4{x^3} - 4\left( 3 \right){x^2} = 4{x^3} - 12{x^2}$
Now again differentiate this equation w.r.t x to get the double differentiation so we have,
$\Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}f'\left( x \right) = \dfrac{d}{{dx}}\left( {4{x^3} - 12{x^2}} \right) = 12{x^2} - 24x$
Now to find the inflection points equate the above equation to zero so we have,
$\Rightarrow f''\left( x \right) = 12{x^2} - 24x = 0$
Now simplify this we have,
$\Rightarrow 12x\left( {x - 2} \right) = 0$
Therefore x = 0, 2
So the inflection points of the given curve is (0, 2)
Now for concave upward
$\Rightarrow f''\left( x \right) > 0$
$\Rightarrow 12x\left( {x - 2} \right) > 0$
$\Rightarrow x\left( {x - 2} \right) > 0$
So to satisfy this condition x should be less either less than 0 or greater than 2.
So the interval of x in which the given function is concave upward is
$\Rightarrow x \in \left( { - \infty ,0} \right) \cup \left( {2,\infty } \right)$
Now for concave downward
$\Rightarrow f''\left( x \right) < 0$
$\Rightarrow 12x\left( {x - 2} \right) < 0$
$\Rightarrow x\left( {x - 2} \right) < 0$
So to satisfy this condition x should be between 0 and 2.
So the interval of x in which the given function is concave downward is
$\Rightarrow x \in \left( {0,2} \right)$
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that to find out the inflection points, double differentiate the given equation and equate to zero and solve for x, for concave up the value of the double differentiation is greater than zero and for concave down the value of the double differentiation is less than zero, so evaluate the intervals as above which is the required answer.