Question

Find the inductance of a unit length of two parallel wires, each of radius $a$ whose centres are at a distance $d$ apart and carry equal currents in opposite directions. Neglect the flux within the wire:
A.$\dfrac{\mu_{0}}{2\pi}ln\left(\dfrac{d-a}{a}\right)$
B. $\dfrac{\mu_{0}}{\pi}ln\left(\dfrac{d-a}{a}\right)$
C. $\dfrac{3\mu_{0}}{\pi}ln\left(\dfrac{d-a}{a}\right)$
D. $\dfrac{\mu_{0}}{3\pi}ln\left(\dfrac{d-a}{a}\right)$

Answer 1

We know that flow of current through a conductor varies the magnetic field around the conductor, the ability of the conductor to resist the change in magnetic field around it is called inductance . Here, we must find the inductance due to two wires.
Formula used:
$B=\dfrac{\mu_{0}I}{2\pi r}$
$d\phi=\dfrac{\mu_{0}I}{2\pi r}\times ldr$
$L=\dfrac{d\phi}{I}$

Complete step-by-step solution:
Consider two parallel straight wire inductors of length $l$ of radius $a$ separated by a distance $d$ as shown in the figure below. Let $\;dr$ be a small region in-between the inductors at a distance $r$ from one inductor.

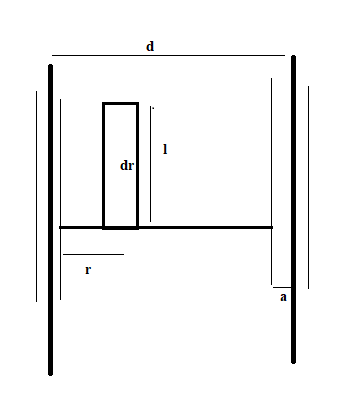
When $I$ current is passed through the wires, there is a magnetic field $B$ produced around the wires . then the magnetic field of a straight wire at a point $dr$ is given as $B=\dfrac{\mu_{0}I}{2\pi r}$, where $\mu_{0}$ is the permeability of the medium.
Then the change in magnetic flux $d\phi$ on the the small region $d\;r$ is given as
$d\phi=B.A=\dfrac{\mu_{0}I}{2\pi r}\times ldr$, where $B$ is the magnetic field and $A$ is the area covered.
Now let us consider the flux between the inductors, due to one inductor,
$\begin{aligned} & \phi =\int\limits_{0}^{{{\phi }_{1}}}{d\phi }=\int\limits_{a}^{d-a}{\dfrac{{{\mu }_{0}}I}{2\pi r}\times ldr} \\\ & \phi =\dfrac{{{\mu }_{0}}Il}{2\pi }\ln \left( \dfrac{d-a}{a} \right) \\\ \end{aligned}$
Since the two inductors are parallel, the flux by the other is also the same. Then the total flux is given as ${{\phi }_{T}}=2\phi =\dfrac{{{\mu }_{0}}Il}{\pi }\ln \left( \dfrac{d-a}{a} \right)$
We know that inductance is $L=\dfrac{{{\phi }_{T}}}{I}$
Then, $L=\dfrac{{{\mu }_{0}}Il}{\pi I}\ln \left( \dfrac{d-a}{a} \right)$
$\therefore L=\dfrac{{{\mu }_{0}}l}{\pi }\ln \left( \dfrac{d-a}{a} \right)$
Thus the correct answer is option B. $\dfrac{\mu_{0}}{\pi}ln\left(\dfrac{d-a}{a}\right)$

Note: Here we can see that the figure has a line of symmetry. Thus we can assume that the flux due to the wires is equal, when we consider the region between the wires. This is a very easy sum, if one knows the related formulas.