Solveeit Logo
Login

Question

Question: Find the inclination of the line passing through (– 5, 3) and (10, 7). (a) 14.73 (b) 14.93 (c...

Find the inclination of the line passing through (– 5, 3) and (10, 7).
(a) 14.73
(b) 14.93
(c) 14.83
(d) 14.63
(e) None of these

Explanation

Solution

To solve this question, we will first of all calculate the equation of the line passing through two given points. If the given points are (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) then the equation of the line passing through (x1,y1),(x2,y2)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right) is y−y1=y2−y1x2−x1(x−x1).y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right). The inclination of the line is given by the slope tan⁡θ=y2−y1x2−x1\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} where θ\theta is the inclination of the line.

Complete step-by-step solution:
Given that the two points are (– 5, 3) and (10, 7). First of all, we will determine the equation of the line passing through the two given points (– 5, 3) and (10, 7). The equation of the line passing through (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) is given by
y−y1=y2−y1x2−x1(x−x1)y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)
So, the equation of the line passing through (– 5, 3) and (10, 7) using the above fact is given by,
(x1,y1)=(−5,3)\left( {{x}_{1}},{{y}_{1}} \right)=\left( -5,3 \right)
(x2,y2)=(10,7)\left( {{x}_{2}},{{y}_{2}} \right)=\left( 10,7 \right)
y−y1=y2−y1x2−x1(x−x1)y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)
⇒y−3=7−310+5(x+5)\Rightarrow y-3=\dfrac{7-3}{10+5}\left( x+5 \right)
⇒y−3=415(x+5)\Rightarrow y-3=\dfrac{4}{15}\left( x+5 \right)
⇒15(y−3)=4(x+5)\Rightarrow 15\left( y-3 \right)=4\left( x+5 \right)
⇒15y−45=4x+20\Rightarrow 15y-45=4x+20
⇒15y−4x=45+20\Rightarrow 15y-4x=45+20
⇒15y−4x=65\Rightarrow 15y-4x=65
This is the equation of the line passing through (x1,y1)=(−5,3)\left( {{x}_{1}},{{y}_{1}} \right)=\left( -5,3 \right) and (x2,y2)=(10,7)\left( {{x}_{2}},{{y}_{2}} \right)=\left( 10,7 \right) is given by 15y−4x=65.15y-4x=65.
Now, the inclination of line or slope of it is given by
tan⁡θ=y2−y1x2−x1\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
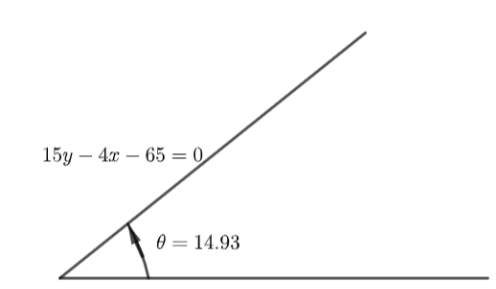
inclination θ=tan⁡−1(y2−y1x2−x1)\text{inclination }\theta ={{\tan }^{-1}}\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)

Substituting the value of x1,y1,x2,y2{{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}} in the above, we get,
tan⁡θ=7−310+5\tan \theta =\dfrac{7-3}{10+5}
⇒tan⁡θ=415\Rightarrow \tan \theta =\dfrac{4}{15}
⇒θ=tan⁡−1(415)\Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{4}{15} \right)
⇒θ=14.93∘\Rightarrow \theta ={{14.93}^{\circ }}
Therefore, the inclination of the line is θ=14.93∘.\theta ={{14.93}^{\circ }}.
Hence, option (b) is the right answer.

Note: The biggest possibility of mistake in this question can be considering the slope=tan⁡θslope=\tan \theta as inclination. This is wrong, tan⁡θ\tan \theta is the slope of the line passing through (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) and inclination given by θ.\theta . If tan⁡θ=m,\tan \theta =m, ⇒θ=tan⁡−1(m)\Rightarrow \theta ={{\tan }^{-1}}\left( m \right) is the inclination.