Question

Find the image of the square PQRS, after the following transformations.
(a) Reflection about PQ
(b) Reflection about PS

Answer 1

Hint : Reflection property in mathematics means finding a mirror image. So we will draw the square PQRS and then analyze how its mirror image will look if we consider PQ as a mirror line. Then we would do the same in case of PS.

Complete step-by-step answer :
Reflection property in mathematics means finding a mirror image.
Observe the diagram

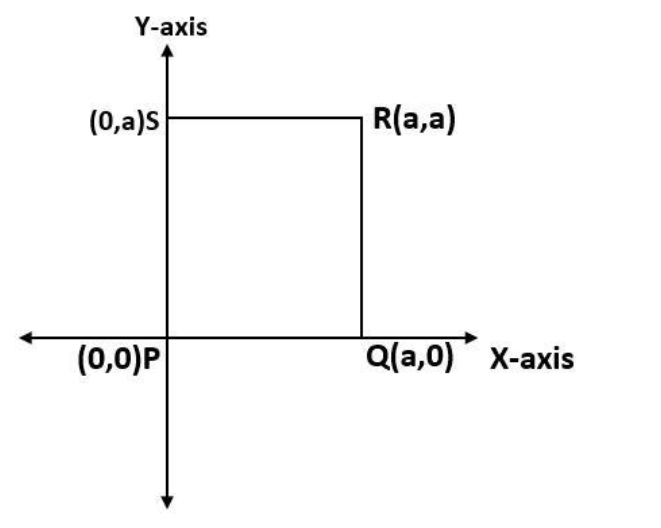
In this diagram, PQRS is a square. For the sake of simplicity, let us consider the square PQRS in a coordinate axis with the coordinates $P(0,0),$ $Q(a,0)$, $R(a,a)$, $S(0, - a)$.
(a) Reflection about PQ
Now, reflection of the square PQRS along PQ means the mirror image of the square PQRS by considering PQ as a mirror line.
For that, the best way is to find the mirror image of every point of the square with respect to the mirror line PQ and then, join the points to get the reflection of the square. Clearly, the mirror image of P and Q with respect to the mirror line, PQ will be P and Q itself as they lie on the line PQ.
Now, for R and S, we need to recall the concept that, mirror image of a point with respect to any line is a point which is at the other side of the line in such a way that the line has the midpoint of the given point and its mirror image. That means, the distance of the image point from the mirror line should be equal and opposite the given point. And also, the line joining the given point and its image point must be perpendicular to the mirror line.
Using this concept, we can say that the image point $R'$ of the point $R(a,a)$ should be equal and opposite the point R. And the line RR’ must be perpendicular to the line PQ.
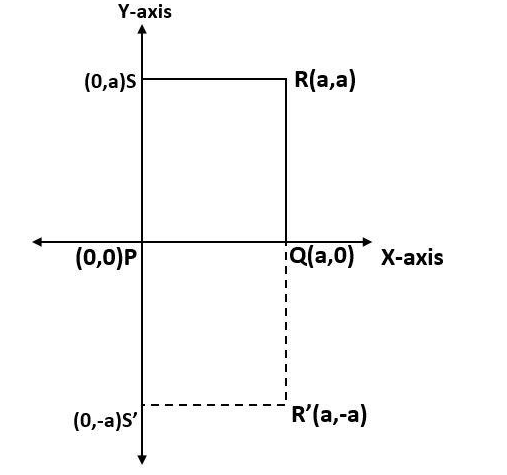
Therefore, the coordinates of the new point $R'$ will be $(a, - a)$.
Similarly, using the same concept, we can say that the coordinates of the image point $S'$ of the point $S(0,a)$, will be $(0, - a)$.
Now plot these points in the coordinate plane and join $PS'R'Q$ to get an image of the square PQRS after the reflection about PQ.
Observe the diagram for reference.

(b) Reflection about PS
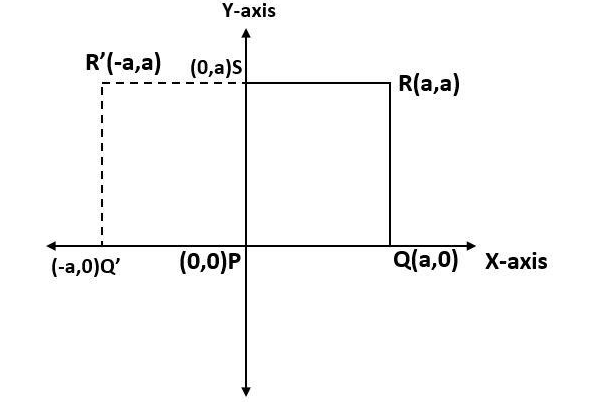
Now, again by using the concept we have used to solve (a), we can find the image points of R and Q with respect to the line PS. And those points will be $R'( - a,a)$ and $Q'( - a,0)$ respectively.
Plot these points in the coordinate plane and join $PQ'R'S$ to get an image of the square PQRS after the reflection about PS.
Observe the diagram for reference.

Note : You can understand the coordinates of P, Q, R, S were in the order given above, because the square has the same length. So all the coordinates need to represent that equal length. Here, the square has length . Assuming the coordinates of all the points of the square made the question comparatively easy.