Question

Find the image of the point $\left( 2,-1,5 \right)$ in the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ . Also, find the length of the perpendicular from the point $\left( 2,-1,5 \right)$ to the line.

Answer 1

Hint : For solving this question first we will take the image of the point $\left( 2,-1,5 \right)$ in the given line in terms of variables and see some important concepts of the 3-D coordinate geometry. Then we will take an arbitrary point on the given line in term of a variable parameter. And as we know that line joining point $\left( 2,-1,5 \right)$ and its foot of perpendicular on the given line will be perpendicular to the given line so, we will use basic vector techniques like if two vectors are perpendicular then their dot product will be zero and distance formula for the 3-D coordinate geometry. After that, we will find the coordinates of the foot of the perpendicular and then apply the midpoint formula to get the image of the point $\left( 2,-1,5 \right)$ in the given line.

Complete step by step solution :
Given:
We have a point $\left( 2,-1,5 \right)$ and we have to find the image of this point in the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ and length of the perpendicular from the point $\left( 2,-1,5 \right)$ to the given line.
Now, let there is a point $A\equiv \left( 2,-1,5 \right)$ and point ${A}'\equiv \left( \alpha ,\beta ,\gamma \right)$ is the image of the point A in the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ .
Now, before we proceed we should know the following concepts of the 3-D co-ordinate geometry:
1. Distance between points $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\text{ and }Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$ and this formula is also called as the distance formula for the 3-D coordinate geometry.
2. If there are two points $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ then, $\overrightarrow{PQ}=\left( {{x}_{2}}-{{x}_{1}} \right)\widehat{i}+\left( {{y}_{2}}-{{y}_{1}} \right)\widehat{j}+\left( {{z}_{2}}-{{z}_{1}} \right)\widehat{k}$ .
3. Equation of a straight line in 3-D passing through a point $\left( a,b,c \right)$ and parallel to a vector $l\widehat{i}+m\widehat{j}+n\widehat{k}$ is given by the equation $\dfrac{x-a}{l}=\dfrac{y-b}{m}=\dfrac{z-c}{n}$ . And coordinates of a general point on the line can be taken as $\left( a+l\lambda ,b+m\lambda ,c+n\lambda \right)$ , where $\lambda$ is a variable parameter.
4. If any two vectors $a\widehat{i}+b\widehat{j}+c\widehat{k}$ and $l\widehat{i}+m\widehat{j}+n\widehat{k}$ are perpendicular. Then, their dot product will be zero, $\left( a\widehat{i}+b\widehat{j}+c\widehat{k} \right)\cdot \left( l\widehat{i}+m\widehat{j}+n\widehat{k} \right)=al+bm+cn=0$ .
5. If there are two points $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ then, coordinates of their midpoint will be $R\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2} \right)$ .
Now, we come back to our question in which we have the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ .
Let, B is a general point on the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ so, according to the third point in the above concepts coordinates of the point B can be written as $B\equiv \left( 11+10\lambda ,-2-4\lambda ,-8-11\lambda \right)$ , where $\lambda$ is a variable parameter and there will be one vector $\overrightarrow{L}=10\widehat{i}-4\widehat{j}-11\widehat{k}$ parallel to the given line.
Now, let point $B\equiv \left( 11+10\lambda ,-2-4\lambda ,-8-11\lambda \right)$ is the foot of the perpendicular of the point $A\equiv \left( 2,-1,5 \right)$on the given line. Then,
$\begin{aligned} & \overrightarrow{AB}=\left( 11+10\lambda -2 \right)\widehat{i}+\left( -2-4\lambda +1 \right)\widehat{j}+\left( -8-11\lambda -5 \right)\widehat{k} \\\ & \Rightarrow \overrightarrow{AB}=\left( 9+10\lambda \right)\widehat{i}-\left( 1+4\lambda \right)\widehat{j}-\left( 13+11\lambda \right)\widehat{k} \\\ \end{aligned}$
Now, as B is the foot of the perpendicular of the point A on the given line and vector $\overrightarrow{L}=10\widehat{i}-4\widehat{j}-11\widehat{k}$ is parallel to the line which means vector $\overrightarrow{AB}$ and $\overrightarrow{L}$ will be perpendicular to each other so, their dot product will be zero. Then,
$\begin{aligned} & \left( \overrightarrow{AB} \right)\cdot \left( \overrightarrow{L} \right)=0 \\\ & \Rightarrow \left( \left( 9+10\lambda \right)\widehat{i}-\left( 1+4\lambda \right)\widehat{j}-\left( 13+11\lambda \right)\widehat{k} \right)\cdot \left( 10\widehat{i}-4\widehat{j}-11\widehat{k} \right)=0 \\\ & \Rightarrow 10\left( 9+10\lambda \right)+4\left( 1+4\lambda \right)+11\left( 13+11\lambda \right)=0 \\\ & \Rightarrow 90+100\lambda +4+16\lambda +143+121\lambda =0 \\\ & \Rightarrow 237+237\lambda =0 \\\ & \Rightarrow \lambda =-1 \\\ \end{aligned}$
Now, from the above result $\lambda =-1$ . Then,
$\begin{aligned} & B\equiv \left( 11+10\lambda ,-2-4\lambda ,-8-11\lambda \right) \\\ & \Rightarrow B\equiv \left( 11-10,-2+4,-8+11 \right) \\\ & \Rightarrow B\equiv \left( 1,2,3 \right) \\\ \end{aligned}$
Now, from the above result, we conclude that the foot of the perpendicular of the point $A\equiv \left( 2,-1,5 \right)$ on the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ will be the point $B\equiv \left( 1,2,3 \right)$ .
Now, length of the AB will be the length of the perpendicular from the point $A\equiv \left( 2,-1,5 \right)$ on the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ so, we can use the distance formula for 3-D coordinate geometry to find the length of the AB. Then,
$\begin{aligned} & AB=\sqrt{{{\left( 1-2 \right)}^{2}}+{{\left( 2+1 \right)}^{2}}+{{\left( 3-5 \right)}^{2}}} \\\ & \Rightarrow AB=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( 3 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\\ & \Rightarrow AB=\sqrt{1+9+4} \\\ & \Rightarrow AB=\sqrt{14}..........................\left( 1 \right) \\\ & \Rightarrow AB\approx 3.7416 \\\ \end{aligned}$
Now, as the point ${A}'\equiv \left( \alpha ,\beta ,\gamma \right)$ is the image of the point $A\equiv \left( 2,-1,5 \right)$ in the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ so, point $B\equiv \left( 1,2,3 \right)$ will be the midpoint of the segment $A{A}'$ . Then,
$\begin{aligned} & B\equiv \left( \dfrac{2+\alpha }{2},\dfrac{\beta -1}{2},\dfrac{\gamma +5}{2} \right)\equiv \left( 1,2,3 \right) \\\ & \Rightarrow \dfrac{2+\alpha }{2}=1 \\\ & \Rightarrow 2+\alpha =2 \\\ & \Rightarrow \alpha =0 \\\ & B\equiv \left( \dfrac{2+\alpha }{2},\dfrac{\beta -1}{2},\dfrac{\gamma +5}{2} \right)\equiv \left( 1,2,3 \right) \\\ & \Rightarrow \dfrac{\beta -1}{2}=2 \\\ & \Rightarrow \beta -1=4 \\\ & \Rightarrow \beta =5 \\\ & B\equiv \left( \dfrac{2+\alpha }{2},\dfrac{\beta -1}{2},\dfrac{\gamma +5}{2} \right)\equiv \left( 1,2,3 \right) \\\ & \Rightarrow \dfrac{\gamma +5}{2}=3 \\\ & \Rightarrow \gamma +5=6 \\\ & \Rightarrow \gamma =1 \\\ \end{aligned}$
Now, from the above result, we conclude that co-ordinates of point ${A}'\equiv \left( \alpha ,\beta ,\gamma \right)$ will be ${A}'\equiv \left( 0,5,1 \right)$ . For more clarity look at the figure given below:

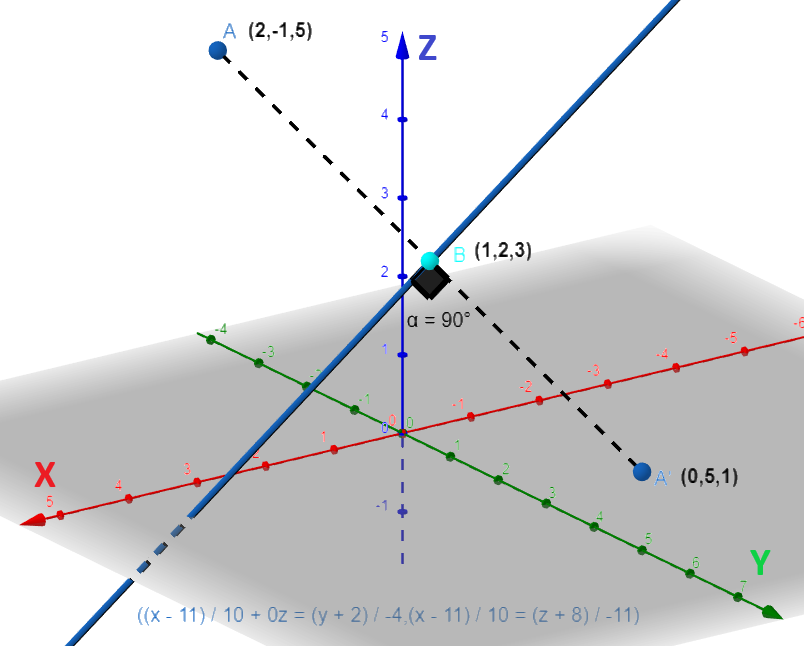
Thus, the image of the point $A\equiv \left( 2,-1,5 \right)$ in the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ will be at point ${A}'\equiv \left( 0,5,1 \right)$ and length of the perpendicular from the point $A\equiv \left( 2,-1,5 \right)$ on the line $\dfrac{x-11}{10}=\dfrac{y+2}{-4}=\dfrac{z+8}{-11}$ will be equal to $AB=\sqrt{14}\text{ units}$ .

Note : While solving this problem, we should remember that the line joining a point with its image is perpendicular to the line about which the image is to be found. Also, the distance between the point and the image is twice the distance between the point and foot on perpendicular from the point to the line about which image is to be found. If we remember these points, then we don’t need to remember the formula. But it is advised to remember the formula, so that time can be saved while solving the problem.