Question

Find the image of point $\left( {3, - 2,1} \right)$ in the plane $3x - y + 4z = 2$.

Answer 1

We will find the equation of the line joining the point and its image. We will assume the midpoint of the line and its image as $T$. We will find the midpoint of the given point and its image using the midpoint formula and equate it with $T$. We will substitute the coordinates of point $T$ in the equation of the plane as that point will lie on the plane. We will find the image by using basic algebra on the linear equation.

Formulas used:
We will use the following formulas:
1. The equation of a line passing through the point $\left( {a,b,c} \right)$ and having direction ratios $p,q$ and $r$ is $\dfrac{{x - a}}{p} = \dfrac{{y - b}}{q} = \dfrac{{z - c}}{r}$ .
2. The midpoint of 2 points $\left( {a,b,c} \right)$ and $\left( {p,q,r} \right)$ is $\left( {\dfrac{{a + p}}{2},\dfrac{{b + q}}{2},\dfrac{{c + r}}{2}} \right)$

Complete step by step solution:
We will first draw the diagram.

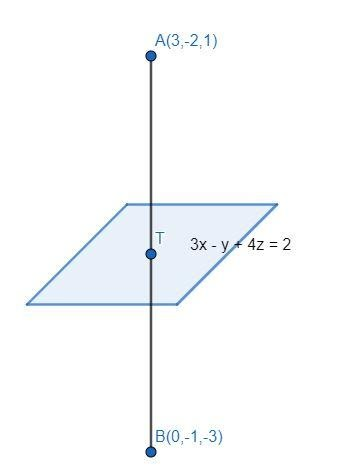
We will assume that the image of point $A\left( {3, - 2,1} \right)$ in the plane $3x - y + 4z = 2$ is point $B$ . The line joining $A$ and $B$ will be normal to the plane $3x - y + 4z = 2$. So, the direction ratios of the line $AB$ will be 3, $- 4$ and 1.
We will formulate the equation of the line $AB$.
Substituting 3 for $a$ , $- 2$ for $b$ , 1 for $c$ , 3 for $p$ , $- 4$ for $q$ and 1 for $r$ in the formula $\dfrac{{x - a}}{p} = \dfrac{{y - b}}{q} = \dfrac{{z - c}}{r}$ , we get
$\dfrac{{x - 3}}{3} = \dfrac{{y - \left( { - 2} \right)}}{{ - 1}} = \dfrac{{z - 1}}{4}$
We will assume that the 3 ratios are equal to $k$, Therefore,
$\Rightarrow \dfrac{{x - 3}}{3} = \dfrac{{y + 2}}{{ - 1}} = \dfrac{{z - 1}}{4} = k$
Now we will find the values of $x,y$ and $z$ in terms of $k$.
So,
$\Rightarrow \dfrac{{x - 3}}{3} = k$
On cross multiplication, we get
$\begin{array}{l} \Rightarrow x - 3 = 3k\\\ \Rightarrow x = 3k + 3\end{array}$
Now equating the $y$ term with $k$, we get
$\Rightarrow \dfrac{{y + 2}}{{ - 1}} = k$
On cross multiplication, we get
$\begin{array}{l} \Rightarrow y + 2 = - 1 \cdot k\\\ \Rightarrow y = - k - 2\end{array}$
Now equating the $y$ term with $k$, we get
$\Rightarrow \dfrac{{z - 1}}{4} = k$
On cross multiplication, we get
$\begin{array}{l} \Rightarrow z - 1 = 4k\\\ \Rightarrow z = 4k + 1\end{array}$
Any point lying on line $AB$ will be of the form $\left( {3k + 3, - k - 2,4k + 1} \right)$.
We will take point $B \equiv \left( {3k + 3, - k - 2,4k + 1} \right)$.
We will assume that point $T$ is the mid-point of line $AB$.
We will find the coordinates of $T$ using the mid-point formula, $\left( {\dfrac{{a + p}}{2},\dfrac{{b + q}}{2},\dfrac{{c + r}}{2}} \right)$. So,
$\begin{array}{l}T \equiv \left( {\dfrac{{3 + 3k + 3}}{2},\dfrac{{ - 2 - k - 2}}{2},\dfrac{{1 + 4k + 1}}{2}} \right)\\\ \Rightarrow T \equiv \left( {\dfrac{3}{2}k + 3, - \dfrac{k}{2} - 2,2k + 1} \right)\end{array}$
We know that point $T$ will lie on the plane $3x - y + 4z = 2$ . It will satisfy the equation of the plane:
$\Rightarrow 3x - y + 4z = 2$
Now substituting the values of $x$, $y$ and $z$, we get
$\Rightarrow 3\left( {\dfrac{3}{2}k + 3} \right) - \left( { - \dfrac{k}{2} - 2} \right) + 4\left( {2k + 1} \right) = 2$
Multiplying the terms, we get
$\Rightarrow \dfrac{9}{2}k + 9 + \dfrac{k}{2} + 2 + 8k + 4 = 2$
Adding the terms, we get
$\begin{array}{l} \Rightarrow 13k = - 13\\\ \Rightarrow k = - 1\end{array}$
We have calculated the value of $k$ .
Now substituting $k = - 1$ in the equation of point $B$, we get
$\begin{array}{l}B = \left( {3\left( { - 1} \right) + 3, - \left( { - 1} \right) - 2,4\left( { - 1} \right) + 1} \right)\\\ \Rightarrow B = \left( {0, - 1, - 3} \right)\end{array}$
$\therefore$ The image of $\left( {3, - 2,1} \right)$ in the plane $3x - y + 4z = 2$ is $\left( {0, - 1, - 3} \right)$ .

Note:
The coefficient of $x,y$ and $z$ in the equation of a plane are the direction ratios of the normal to the plane. That is why we have taken the direction ratios of line $AB$ as 3, $- 1$ and 4.
Direction ratios are also known as direction component or direction numbers. It can be said that direction ratios are the numbers proportional to direction cosines.