Question
Question: Find the horizontal and vertical components of the \[100m\] displacement of a superhero who flies fr...
Find the horizontal and vertical components of the 100m displacement of a superhero who flies from the top of a tall building following the path shown in the above figure:
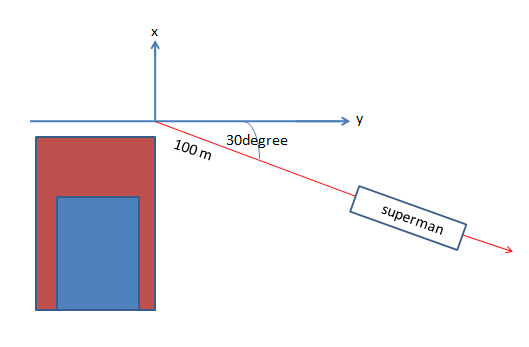
Solution
A vector can be divided into two components along two perpendicular axes, those are called the rectangular components. Since the displacement is a vector quantity it also has the resolution along two axes. The values of the two components are cosine and sine of the angle multiplied with the magnitude of the vector. Note that, here the angle is the angle between the vector and the horizontal component.
Complete step by step answer:
In a two-dimensional coordinate system, any vector is broken into x -component and y -component. for instance, the vector V is broken into 2 elements, Vx and Vy . If the angle between the vector and its x -component be θ
Vx=Vcosθ
Vy=Vsinθ
Here, displacement is a vector quantity. Let, the displacement vector is . given that, the angle between the vector and its x -component be θ=30∘
vector S is broken into two elements, Sx and Sy.
Sx=Scosθand Sy=Ssinθ
Given, the magnitude of , S=100
So, Sx=Scosθ=100cos30∘
⇒Sx=100×23
⇒Sx=503
And, Sy=Ssinθ=100sin30∘
⇒Sy=100×21
⇒Sy=50
Hence, the horizontal and vertical components of the 100m displacement will be ⇒Sx=503 and ⇒Sy=50respectively.
Note: If we want to break the vector V along this vector itself i.e along the vector V, the angle between the vector and its x -component will be θ=0∘,
Such as, Vx=Vcos0∘=0
And, the vertical component will be Vy=Vsin0∘=0
From these we can conclude:
The value of the component of a vector along this particular vector will be the same as the magnitude of the vector.
There will be no vertical component of the vector in this case.
