Question

Find the height of a vertical cliff if the angle of elevation from a point 318 m from the base of the cliff is $23^\circ$ .

Answer 1

Hint : Here, first of all let the height of the vertical cliff be h. Now, draw the figure for the given problem statement. Now, as we know that in a right angled triangle,
$\Rightarrow \tan \theta = \dfrac{{opposite}}{{adjacent}}$
And we have the value of $\theta$ and adjacent, so we can easily find the height of the cliff.

Complete step-by-step answer :
In this question, we are given a point 318 m away from the base of a vertical cliff and the angle of elevation from that point is $23^\circ$ and we need to find the height of the vertical cliff.
Given data:
Let us draw the figure for the given problem.
Let point C be the point 318 m away from the foot of the vertical cliff. Let the foot of the vertical cliff be B.
Let the height of the vertical cliff be h and the angle of elevation $23^\circ$ .
Therefore, the figure will be

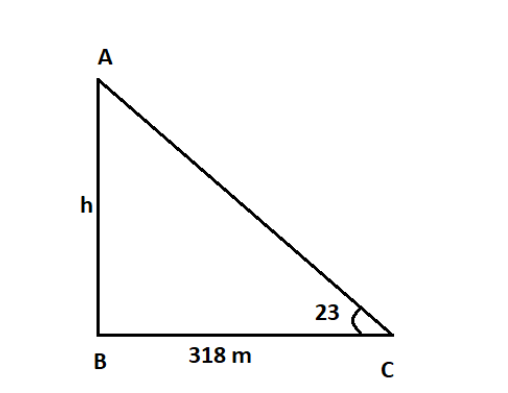
Here,
$BC =$ Distance between the point and the foot of vertical cliff $= 318m$
$AB =$ Height of cliff $= h$
$\angle AOB =$ Angle of elevation $= 23^\circ$
Now, in right angled $\Delta ABC$ , we know that
$\Rightarrow \tan \theta = \dfrac{{opposite}}{{adjacent}} = \dfrac{{AB}}{{BC}}$
Therefore,
$\Rightarrow \tan 23^\circ = \dfrac{h}{{318}} \\\ \Rightarrow h = 318 \times \tan 23^\circ \;$
Now, we know that $\tan 23^\circ = 0.4244$ . Therefore,
$\Rightarrow h = 318 \times 0.4244 \\\ \Rightarrow h = 134.95m \;$
Hence, the height of the vertical cliff is 134.95m.
So, the correct answer is “134.95 m”.

Note : Here, note that the difference between angle of elevation and angle of depression is that the angle of elevation is the angle made by the horizontal line and line of sight. The angle of depression is also the angle formed by the horizontal line and the object's line of sight but the object is at some height h.