Question
Question: Find the gravitational force acting on a particle A inside a uniform spherical layer of matter....
Find the gravitational force acting on a particle A inside a uniform spherical layer of matter.
Solution
Divide the sphere into thin spherical shells and find the force acting on the particle lying inside the sphere by a thin spherical shell and integrate within the suitable limits.
Complete step by step solution:
Let M be the mass of the uniform spherical layer of matter and m be the mass of the particle lying inside it at a distance of r from the centre. Let the sphere be divided into thin spherical shells of density σ per unit area. Force acting on the particle by a thin spherical shell of radius R is given by
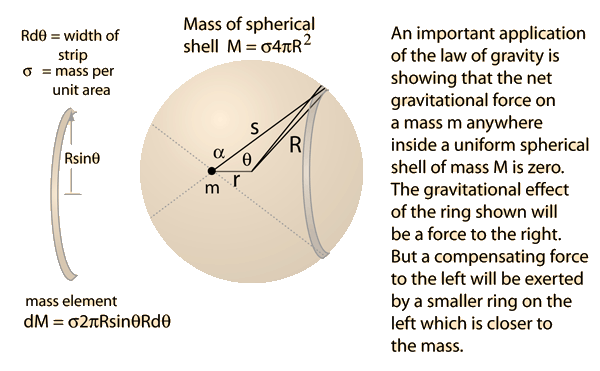
dF=s2GmdMcosα
Mass =dM=σ2πRsinθRdθ
The force from the entire spherical shell is given by
F=2πGσmR2θ=0∫πs2cosαsinθdθ -----(1)
In order to find the value of the integral we need to express in terms of. To do so we use cosine formula. Using the cosine law, we have s2=R2+r2θ−2Rrcosθ
Differentiating both sides, we get
2sds=2Rrsinθdθ
⇒sinθdθ=Rrsds ------------(2)
Now using the cosine formula for the external angle
R2=r2+s2−2rscosα
cosα=2rsr2+s2−R2 ------------(3)
cosα=2rsr2+s2−R2 ------------(3)
Now, put the values of equations (2) and (3) in equation (1). Also, forθ=0,s=R−rand for θ=π,s=r+R
Now (1) reduces to
F=−2πGσmR2s=R−r∫s=R+rs2.2rs.Rr(r2+s2−R2)sds
⇒F=r2−πGσmR2s=R−r∫s=R+r(1+s2r2−R2)ds
Using the area density expression ⇒σ=4πR2M the above equation reduces to
F=4Rr2−GmMs=R−r∫s=R+r(1+s2r2−R2)ds
⇒F=4Rr2−GmM[s−(r2−R2)s1]s=R−rs=R+r
⇒F=4Rr2−GmM[(R+r)−(R−r)−(r2−R2)(R+r1−R−r1)]
⇒F=4Rr2−GmM[(2r)+(−2r)]⇒F=0
Thus the algebraic sum of the forces acting on the particle lying inside a sphere is zero.
Note: The gravitational force acting on a particle lying inside a spherical layer of matter is always zero. This is true for all particles lying inside a sphere.
