Question

Find the general solution of $\cos \left( \text{x}+\dfrac{\pi }{10} \right)=0$

Answer 1

Hint : We will first define what is the general solution and see the general solutions of various trigonometric ratios. Then, to get the general solution of $\cos \left( \text{x}+\dfrac{\pi }{10} \right)=0$ , we will first find the general solution of cosA = 0, by finding all the possible values for the angle A. Then, we will replace A with $x+\dfrac{\pi }{10}$ and find all the possible value of x but performing mathematical operation.

Complete step-by-step answer :
Trigonometric functions are periodic functions and thus can give same output for various inputs. The periodic property of the sine function can be seen in the diagram below.

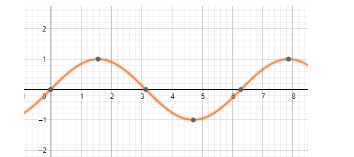
As we can see, there are multiple values of x, for which the value of y is 0.
Thus, no single value of x can justify sinx = 0
Therefore, we find the general value of angle for the trigonometric ratios.
The general value of A for sinA = 0 is $n\pi$ , where n is an integer.
The value of cosA is 0 when A = $\text{A = }-\dfrac{\pi }{2},\dfrac{\pi }{2},\dfrac{3\pi }{2},...$
Thus, the general solution of $\text{A}=\left( 2n+1 \right)\dfrac{\pi }{2}$ , where n is any integer, negative or positive.
Now, we will replace A with $x+\dfrac{\pi }{10}$
$\Rightarrow$ $x+\dfrac{\pi }{10}=\left( 2n+1 \right)\dfrac{\pi }{2}$
First of all, we will solve the parenthesis.
$\Rightarrow$ $x+\dfrac{\pi }{10}=2n\dfrac{\pi }{2}+\dfrac{\pi }{2}$
Now, we will take $\dfrac{\pi }{10}$ on the other side and subtract it from $\dfrac{\pi }{2}$
$\Rightarrow$ $x=2n\dfrac{\pi }{2}+\dfrac{\pi }{2}-\dfrac{\pi }{10}$
$\Rightarrow$ $x=n\pi +\dfrac{2\pi }{5}$
Therefore, the general solution of $\cos \left( \text{x}+\dfrac{\pi }{10} \right)=0$ is given as $n\pi +\dfrac{2\pi }{5}$ , where n is any integer.

Note : Students are encouraged to substitute $x=n\pi +\dfrac{2\pi }{5}$ in $\cos \left( \text{x}+\dfrac{\pi }{10} \right)$ with various values of n. n can only be integer. If the expression yields 0, our solution is correct. It is a good practice to verify the solution when options are not given.