Question
Question: Find the fourth proportional to $(a + b)^2 \times (a^3 - b^3), (a^3 + b^3), (a^2 - b^2)$....
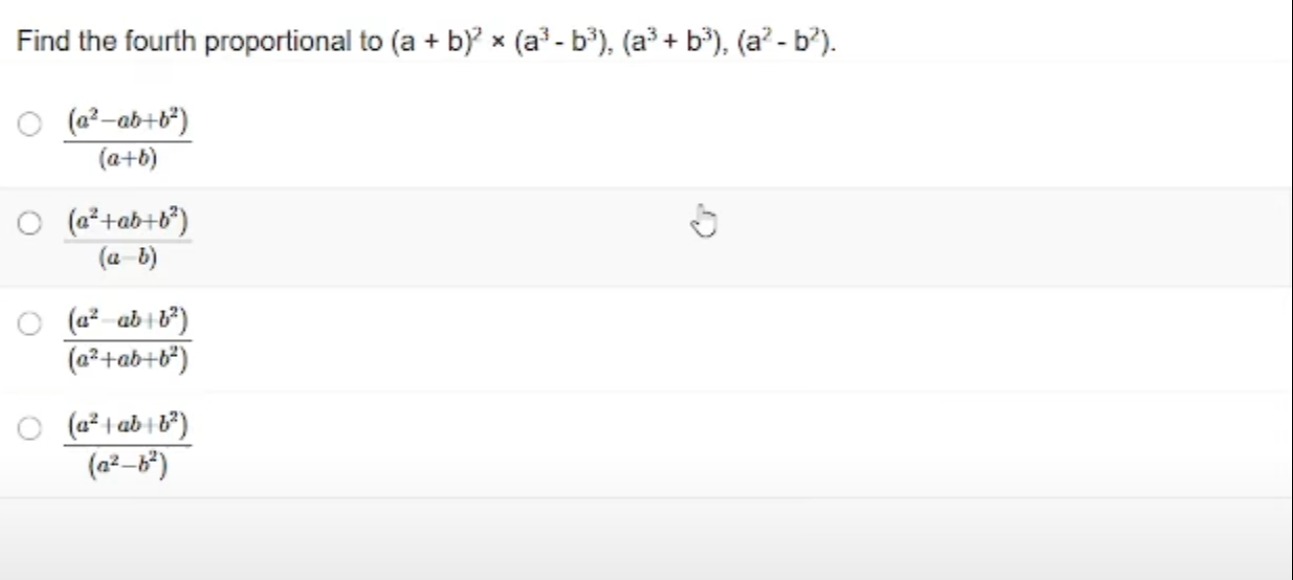
Find the fourth proportional to (a+b)2×(a3−b3),(a3+b3),(a2−b2).
A
(a+b)(a2−ab+b2)
B
(a−b)(a2+ab+b2)
C
(a2+ab+b2)(a2−ab+b2)
D
(a2−b2)(a2+ab+b2)
Answer
(a2+ab+b2)(a2−ab+b2)
Explanation
Solution
To find the fourth proportional X to P=(a+b)2(a3−b3), Q=(a3+b3), and R=(a2−b2), we use the relationship QP=XR. Solving for X, we have X=PQ×R.
Substituting the given expressions: X=(a+b)2(a3−b3)(a3+b3)(a2−b2)
Now we factorize using algebraic identities:
- a3+b3=(a+b)(a2−ab+b2)
- a2−b2=(a−b)(a+b)
- a3−b3=(a−b)(a2+ab+b2)
Substituting these factorizations into the expression for X:
X=(a+b)2×[(a−b)(a2+ab+b2)][(a+b)(a2−ab+b2)]×[(a−b)(a+b)]
Simplifying the numerator: (a+b)(a+b)=(a+b)2.
X=(a+b)2(a−b)(a2+ab+b2)(a+b)2(a−b)(a2−ab+b2)
Canceling common terms (a+b)2 and (a−b) from numerator and denominator yields:
X=(a2+ab+b2)(a2−ab+b2)
