Question

Find the force of friction between the box and inclined plane if the mass of the wooden block is 8 Kg which slides down on an inclined plane with the inclination of $30^\circ$ to the horizontal with a constant acceleration of 0.4$m{s^{ - 2}}$. [g=10$m{s^{ - 2}}$ ].
A. 12.2N
B. 24.4N
C. 36.8N
D. 48.8N

Answer 1

The component of $mg$ along the inclined plane is$mg\sin \theta$ and the block slides down with the net force $ma$. Now, find the normal acting on the block by the plane. Now, use the formula –
$a = g\sin \theta - \mu g\cos \theta$
Where,
$a$= Net acceleration of the block
$\mu$= Coefficient of friction
$\theta$= Angle of inclined plane

Complete step by step answer:
According to the question, it is given that -
Mass of the block $= m = 8kg$
Net acceleration of the block down the plane$= a = 0.4m{s^{ - 2}}$
Angle of inclination $= \theta = {30^ \circ }$
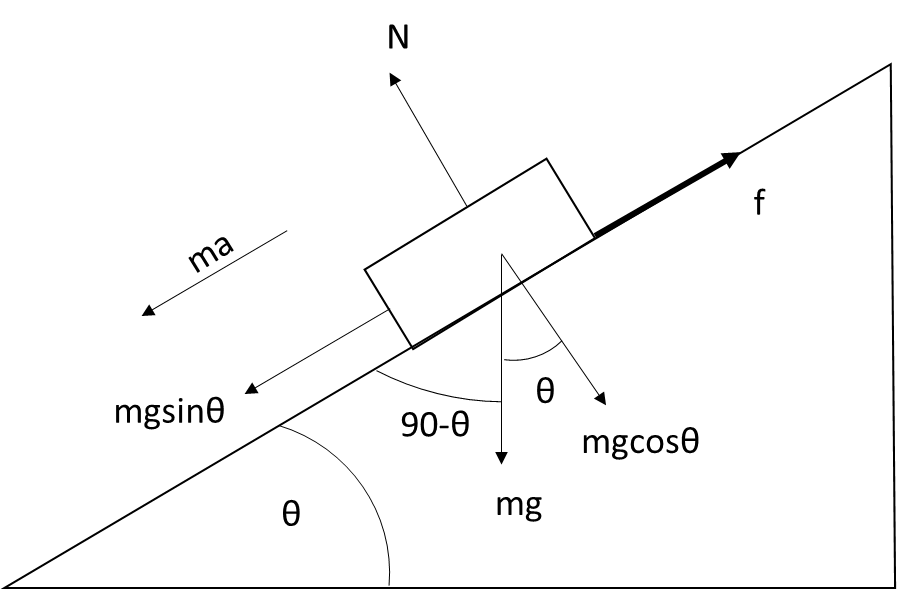
Value of acceleration due to gravity = g = 10$$$m{s^{ - 2}}$$ Let the force of friction = $$f$$ Let the coefficient of friction= $$\mu $$ We have to find the force of friction $$f$$ Let us understand this problem with the help of a diagram  From the above diagram, we can conclude that the inclined plane makes an angle $$\theta $$with the horizontal As the block acts downwards vertically so, the weight of the block ismg$. The component of$mgalong the inclined plane is $$mg\sin \theta $$ & perpendicular to the Inclined plane is $$mg\cos \theta $$. From the definition of frictional force, we know that frictional forcefalways opposes the relative motion of the block so it will act along the inclined plane upwards The frictional force is given by $$f = \mu N$$ Where $$N$$ is the normal reaction on the block by the plane which acts perpendicular to it and\mu is the coefficient of friction. Also, from the figure, the block is sliding down with a net force $$ma$$ Where, $$a$$ is net acceleration Writing force equations along the inclined plane & considering downward inclined direction as positive, we get – $$\Rightarrow mg\sin \theta - f = ma$$ ………………...(1) We know that – $$f = \mu N$$ Putting value of $$f$$ in equation (1) we get $$\Rightarrow mg\sin \theta - \mu N = ma$$ ……………………….(2) Writing force equations perpendicular to the inclined plane & considering perpendicular upward inclined direction as positive we get. $$N = mg\cos \theta $$ Putting value of $$N$$ in equation (2) we get $$\Rightarrow mg\sin \theta - \mu mg\cos \theta = ma$$ $$\Rightarrow a = g\sin \theta - \mu g\cos \theta $$ Putting the values ofg$,$a$, $\theta$ in above equation
$\Rightarrow 0.4 = 10\sin {30^0} - \mu 10\cos {30^0}$ ($\sin {30^0} = \dfrac{1}{2}$,$\cos {30^0} = \dfrac{{\sqrt 3 }}{2}$)
$\Rightarrow \mu \dfrac{{10\sqrt 3 }}{2} = \dfrac{{10}}{2} - 0.4$
Solving the above we get
$\Rightarrow \mu$=0.53 (It is a dimensionless quantity)
Now using $f = \mu N$ & $N = mg\cos \theta$
$\Rightarrow f = \mu mg\cos \theta$
$\Rightarrow f = 0.53 \times 8 \times 10 \times \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow f = 36.8N$

$\therefore$ The force of friction between the box and inclined plane 36.8N. Hence, option (C) is correct.

Note:
This problem could also have been solved directly from equation (1)
$mg\sin \theta - f = ma$
$\Rightarrow f = ma - mg\sin \theta$
$\Rightarrow f = 8 \times 0.4 - 8 \times 10\sin {30^0}$
$\Rightarrow f = 8 \times 0.4 - 8 \times 10 \times \dfrac{1}{2}$
$\Rightarrow f = - 36.8N$
Here, the negative sign shows friction acts opposite to the direction of motion.