Question

Find the force of attraction on a particle of mass m placed at the center of a semicircular wire of length L and mass M.

Answer 1

We know the formula to calculate the gravitational force of attraction between two particles. We can use this here by considering that the semicircular wire is made up of many small segments.

Formula used:
$F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$

Complete step by step solution:

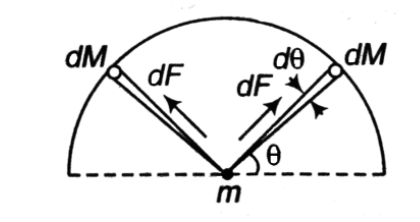
Here we will consider that the semicircular wire is made up of many small element of mass dM, length dx and subtending an angle of $d\theta$and applying the force of dF
So, we can find the force due to one small element and integrate it over the whole semicircular wire, in our case we will find summation of force due to half semicircle and double it as it will make the calculation less complex.
Mass of ‘L’ length wire is given to be M
So, the mass of dx element will be $\dfrac{M}{L}dx = \dfrac{M}{L}Rd\theta = dm$
As dx is the arc length we can write it as product of angle and radius
We know that the force of attraction between any two particles of mass ${m_1}$ and ${m_2}$ kept at
a distance of r is given by
$F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$ where G is the gravitational constant
Similarly, the force of attraction on the particle kept at the center due to semicircular wire is given by
$F = G\dfrac{{Mdm}}{{{r^2}}} = \dfrac{{GmMRd\theta }}{{L{R^2}}} = \dfrac{{GMmd\theta }}{{LR}}$
Now let us see the force of attraction, the force of attraction will be having two components $F\sin \theta$ along the vertical direction and $F\cos \theta$ along the horizontal direction.
Since for the semicircular wire, the horizontal components will cancel each other as they will be equal in magnitude and opposite in direction. So due to small element,
$dF = \dfrac{{2GMm}}{{LR}}\sin \theta d\theta$
$\Rightarrow \int d F = \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{2GMm}}{{LR}}} \sin \theta d\theta = \dfrac{{2GMm}}{{LR}}| - \cos \theta |_0^{\dfrac{\pi }{2}}$
$\Rightarrow F = \dfrac{{2GMm}}{{LR}}$
We know that the circumference of this semicircular wire is its length hence,
$L = \pi R \Rightarrow R = \dfrac{L}{\pi }$ , putting it in the equation,
$\Rightarrow F = \dfrac{{2GMm}}{{L \times \dfrac{L}{\pi }}} = \dfrac{{2\pi GMm}}{{{L^2}}}$
This is the final expression for the force of attraction.

Note:
The gravitational force is always attractive in nature and does not depend on the properties of the medium. They are also central in nature which means that it acts along the line which joins the centre of the two bodies between which it is calculated.