Question
Question: Find the force experienced by the semicircular rod having a charge q, as shown in figure. Radius of ...
Find the force experienced by the semicircular rod having a charge q, as shown in figure. Radius of the wire is R and the line of charge with linear density λ passes through its centre and is perpendicular to the plane of wire.
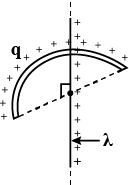
a)2π2εoRλq
b) π2εoRλq
c) 4π2εoRλq
d)8π2εoRλq
Solution
Here in this question we will use the concept of electric field due to infinite linear charge wire and concept of electric field calculation when point charge is not given then we will take a small portion and find the magnitude of charge on that portion then integrate that portion to get the complete calculation of electric field.
Complete step-by-step answer:
An infinite linear charge wire is given having linear charge density λ. We will first calculate the electric field due to this linear charge at Point P which is at perpendicular R from the charge wire. Electric field can be expressed as -
E=2πε0Rλ Equation1 The direction of electric field is outwards because linear charge wire has positive charge density on it.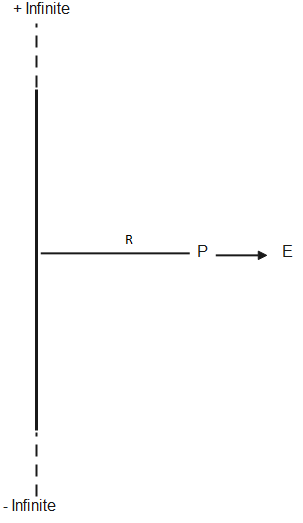
Now we will assume a semi circular ring of radius R having charge q distributed over it. We know that wire is passing through its centre O and perpendicular to its plane. Consider to reference axis X and Y.
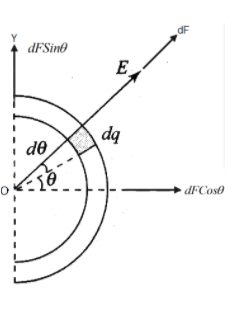
Since there is no point charge so the direct formula of the electric field is not applicable, here q charge is distributed over a semicircular ring so we have to consider a small element having small charge dq and length of this small element is calculated asRdθ. This above value is calculated from the relation
Angle=RadiusArc
⇒Arc=Angle×Radius
∴Arc=Rdθ The value of this dq is calculated by applying a unitary method.
Whole Semi Circular Ring of length πR carries charge =q 1 Unit length of that ring carry charge = πRq
Rdθ length of a small element carries charge = πRq×Rdθ.
So value of dq=πRq×Rdθ
⇒dq=πqdθ.Equation2
Since wire is passed through the centre of semi circular rod and wire is having positive charge so electric field due to this wire is outwards as shown in the figure and semi circular rod is also having positive charge so direction of force is also outwards. Due to this electric field of wire force on small elements dq is also small and can be represented by dF.
So value of this force acting on small element will be dF=Edq Put the value of the electric field from equation 1.
So it becomes dF=2πε0Rλdq Equation3
This force is now resolved in two components: - 1. dFCosθ(Along X axis)
2. dFSinθ(Along Y axis) Now if we consider same small element on other side of semicircular rod then same components are resolved and dFSinθis in opposite direction so it is cancel out and only effective component exist for this whole semicircular rod is dFCosθ.
So to calculate net force we have to integrate this dFCosθfrom 0 to π/2 on one side and then double it to get force due to the other side also. So net force will be Fnet=20∫π/2dFCosθ
Put the value of dF from equation 3 then we get ⇒Fnet=20∫π/22πε0RλdqCosθ Put the value of dq from equation 2, we get
⇒Fnet=20∫π/22πε0RλπqdθCosθ
⇒Fnet=π2ε0Rqλ0∫π/2Cosθdθ ⇒Fnet=π2ε0Rqλ[Sinθ]π/20 ⇒Fnet=π2ε0Rqλ[Sin2π−Sin0] ⇒Fnet=π2ε0Rqλ[1−0]
∴Fnet=π2ε0Rqλ Correct Option is B.
So, the correct answer is “Option B”.
Note: In such a type of question basic thing we have to remember about charge distribution. Whenever this continuous charge distribution is given then the principle of superposition is not applied, this principle is only applied when discrete charge distribution is given. Here in this question linear charge distribution is given so the principle of superposition cannot be applied.
