Question

Find the exact value of the six trigonometric functions of $\theta$ for the point$\left( { - 4, - 6} \right)$.

Answer 1

We know that for a right angled triangle with angle $\theta$

$$\sin \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\\ \cos \theta = \dfrac{{{\text{adjacent}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\\ \tan \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{adjacent}}\;{\text{side}}}} \\\$$

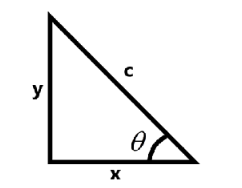
So by using the above relations and other basic trigonometric identities we can find all the six trigonometric functions of $\theta$for the point$\left( { - 4, - 6} \right)$.

Complete step by step solution:
Given
$\left( { - 4, - 6} \right)..................................\left( i \right)$
Now as given in (i) we have the point $\left( { - 4, - 6} \right)$ at which we have to find the all 6 trigonometric functions.
So in order to find the 6 trigonometric functions at $\left( { - 4, - 6} \right)$ we first have to construct a right angled triangle.
So for constructing a right angled triangle let us take:
$x = - 4 \\\ y = - 6 \\\$

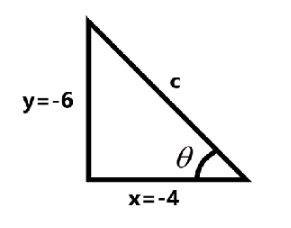
Such that we have to find$c$.
Also by Pythagoras theorem we can write:
${x^2} + {y^2} = {c^2}......................\left( {ii} \right)$
On substituting $x\;{\text{and}}\;y$we can write:
${\left( { - 4} \right)^2} + {\left( { - 6} \right)^2} = {c^2} \\\ \Rightarrow {c^2} = {\left( { - 4} \right)^2} + \left( { - 6} \right) \\\ \Rightarrow {c^2} = 16 + 36 \\\ \Rightarrow {c^2} = 52 \\\ \Rightarrow c = 2\sqrt {13} .........................\left( {iii} \right) \\\$
Now we have:
${\text{adjacent}}\;{\text{side}} = - 4 \\\ {\text{opposite}}\;{\text{side}}\; = - 6 \\\ {\text{hypotenuse}}\; = 2\sqrt {13} \\\$
So in order to find the first 3 basic trigonometric functions we have the formulas:

$$\sin \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\\ \cos \theta = \dfrac{{{\text{adjacent}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\\ \tan \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{adjacent}}\;{\text{side}}}} \\\$$

On substituting the values we have found from the right angled triangle we get:

$$\sin \theta = \dfrac{{ - 6}}{{2\sqrt {13} }} = - \dfrac{3}{{\sqrt {13} }} = - 3\dfrac{{\sqrt {13} }}{{13}} \\\ \cos \theta = \dfrac{{ - 4}}{{2\sqrt {13} }} = - \dfrac{2}{{\sqrt {13} }} = - 2\dfrac{{\sqrt {13} }}{{13}} \\\ \tan \theta = \dfrac{{ - 6}}{{ - 4}} = \dfrac{3}{2} \\\$$

Since the other 3 trigonometric functions are inverse in nature to the above mentioned trigonometric functions, we just have to take the reciprocal of the above found values.
Now to find the other 3 trigonometric formulas we have the formulas:

$${\text{cosec}}\theta = \dfrac{1}{{\sin \theta }} \\\ \sec \theta = \dfrac{1}{{\cos \theta }} \\\ \cot \theta = \dfrac{1}{{\tan \theta }} \\\$$

On substituting we get:

$${\text{cosec}}\theta = \dfrac{1}{{\sin \theta }} = - \dfrac{{13}}{{3 \times \sqrt {13} }} = - \dfrac{{\sqrt {13} }}{3} \\\ \sec \theta = \dfrac{1}{{\cos \theta }} = - \dfrac{{13}}{{2 \times \sqrt {13} }} = - \dfrac{{\sqrt {13} }}{2} \\\ \cot \theta = \dfrac{1}{{\tan \theta }} = \dfrac{2}{3} \\\$$

Now we have found the values of all the 6 trigonometric formulas.
**Therefore our six trigonometric functions of $\theta$ for the point $\left( { - 4, - 6} \right)$ are:

\sin \theta = - 3\dfrac{{\sqrt {13} }}{{13}} \\\ \cos \theta = - 2\dfrac{{\sqrt {13} }}{{13}} \\\ \tan \theta = \dfrac{3}{2} \\\ {\text{cosec}}\theta = - \dfrac{{\sqrt {13} }}{3} \\\ \sec \theta = - \dfrac{{\sqrt {13} }}{2} \\\ \cot \theta = \dfrac{2}{3} \\\ $$** **Note:** Some other equations needed for solving trigonometric problems are: $$\begin{array}{*{20}{l}} {\sin \left( {2\theta } \right) = 2\sin \left( \theta \right)\cos \left( \theta \right)} \\\ {\cos \left( {2\theta } \right) = {{\cos }^2}\left( \theta \right)-{{\sin }^2}\left( \theta \right) = 1- 2{\text{ }}{{\sin }^2}\left( \theta \right) = 2{\text{ }}{{\cos }^2}\left( \theta \right)-1} \end{array}$$ While solving problems similar to the above ones one should take care while forming the triangle and finding the values of its sides. Also while representing the values of trigonometric functions one should not forget to rationalize the denominator.