Question

Find the exact value of $\cos \left( {\dfrac{\pi }{4}} \right)$?

Answer 1

This problem deals with finding the exact value of $\cos \left( {\dfrac{\pi }{4}} \right)$, by the help of a right angled triangle. As we know that trigonometry is only applicable for the right angled triangle. Given the cosine of a particular angle. The given angle is in the units of radians, we have to convert the given angle to the units of radians, and then proceed to find the exact value of the angle.

Complete step by step answer:
Here it is possible to find the exact value of $\cos \left( {\dfrac{\pi }{4}} \right)$ by constructing a right angled triangle with one angle set to $\dfrac{\pi }{4}$ radians.
First converting the angle in radians to degrees.
$\Rightarrow$1 radian = $\dfrac{{180}}{\pi }$ degrees.
Given $\dfrac{\pi }{4}$ radians, which is converted to degrees, as shown below:
$\Rightarrow \dfrac{\pi }{4}$radian = $\dfrac{\pi }{4} \times \dfrac{{180}}{\pi }$ degrees.
$\therefore \dfrac{\pi }{4}$ radian = ${45^ \circ }$
Consider a right angled triangle with one of the acute angles set to ${45^ \circ }$. To make the sum of all the angles in a triangle, hence the other acute angle is also ${45^ \circ }$. As both angles are equal it is a right angled triangle.

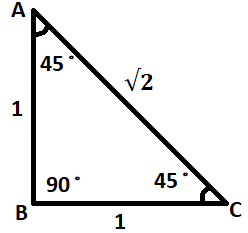
Let the lengths of the base and the height of the triangle are 1, 1 whereas the hypotenuse length is $\sqrt 2$. By applying the Pythagoras theorem.
Now as we know that cosine trigonometric is given by the ratio of the base to the hypotenuse, as given:
$\therefore \cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$

Note: Please note that trigonometry can be applied only to right triangles, and as one of the angle is ${45^ \circ }$, the other angle is also ${45^ \circ }$, as the angles in a triangle are supplementary, and also we can deduce that it is also an isosceles triangle, as there two equal sides corresponding two equal angles, hence it is a right isosceles triangle.