Question

Find the equivalent resistance between X and Y.

$\begin{aligned} & A.R \\\ & B.\dfrac{R}{L} \\\ & C.2R \\\ & D.5R \\\ \end{aligned}$

Answer 1

Hint: We will apply the Wheatstone bridge principle in order to solve this question. First modify the given circuit, that is, combine all series circuits together. Remember the equilibrium condition of the bridge is satisfied, no current will flow through this central resistance. Then apply the formula, for parallel resistance.

Formula used:
$\dfrac{1}{R^\prime}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$

Complete step-by-step solution:
First, we will modify the circuit to make it look simpler.
Let's put the x and y points as far as possible.

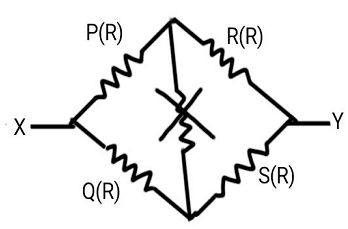
Look at the given image to have a better understanding. Then it looks like a Wheatstone bridge. Now the four resistances of a Wheatstone bridge are denoted by P, Q, R and S. The resistance in the center of this bridge may be anything. Now if the equilibrium condition of the bridge is satisfied, no current will flow through this central resistance at all. The condition for this equilibrium of the Wheatstone bridge is given by,
$\dfrac{P}{Q}=\dfrac{R}{S}$
Here, the resistance of the four arms of the bridge are all equal. So, this condition is satisfied very well. So, when a voltage is applied across x and y, no current will flow through the central resistance. Therefore, we can neglect the resistance present in the center of the bridge.
So, after neglecting the middle resistance, the total resistance on the upper side is 2R (Since they are in series combination).
Similarly, the total resistance on the lower part is 2R (Since they two are in series combination).
Now, the equivalent resistance of two resistances of 2R, connected in parallel is given by,
$\begin{aligned} & \dfrac{1}{{{R}^{\prime }}}=\dfrac{1}{2R}+\dfrac{1}{2R} \\\ & \Rightarrow \dfrac{1}{{{R}^{\prime }}}=\dfrac{2}{2R}=\dfrac{1}{R} \\\ \end{aligned}$
${{R}^{\prime }}=R$
So, the equivalent resistance is R, and option A is the correct answer.

Additional information:
Wheatstone bridge is widely used in determination of unknown resistance. The practical instruments where this principle is used are Metre Bridge, Post Office Box etc.

Note: Even if all the resistances were not equal, but the Wheatstone bridge principle were satisfied you could easily omit the resistance present in the center. Omitting a resistance here does not mean to replace it by a resistance less wire. Another way is to use Kirchhoff's law, but it will become complicated.