Question

Find the equivalent resistance between the points a and b.

Answer 1

We will apply the Wheatstone bridge principle in order to solve this question. Firstly, combine the series resistances and form the ideal circuit of a Wheatstone bridge. Just keep in mind no current will flow through the central resistance. Then apply the formula and find the answer.

Formula used:
$R = {R_1} + {R_2}$ when connected in series
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ when in parallel.

Complete step by step answer:
Modifying the above diagram, we converted it into the Wheatstone bridge as shown below.From the question circuit, we come to know that the $4\Omega ,2\Omega$ these are parallelly connected and $8\Omega ,4\Omega$ are also parallelly connected. So, we join them one up and one down and $10\Omega$ is the middle resistance.

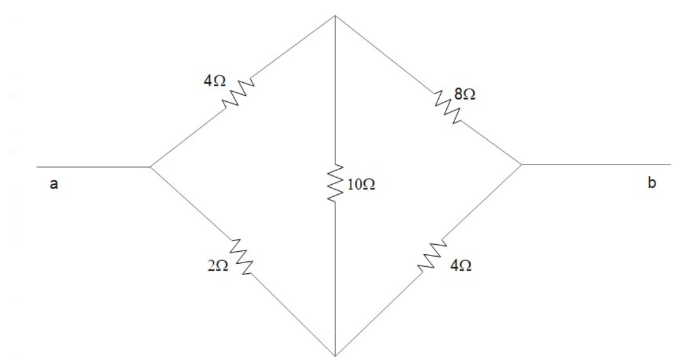
Now, the condition for the Wheatstone bridge is satisfied as $\dfrac{P}{Q} = \dfrac{R}{S}$ where P, Q, R, S are the sides of the bridge. From our diagram, $\dfrac{4}{2} = \dfrac{8}{4}$ so it satisfies the condition for Wheatstone bridge. And no current is followed through the central resistance. So, neglecting the middle resistance.
Now, total resistance of the upper side is $12\Omega$ (since they are in series combination)
Similarly, total resistance in the lower part is $6\Omega$ (these too are in series combination)
Hence, equivalent resistance be given as
$\dfrac{1}{R} = \dfrac{1}{6} + \dfrac{1}{{12}}$
$\therefore R = 4\Omega$

Thus, the equivalent resistance is $4\Omega$.

Note: We can easily omit the resistance connected in the center. Omitting here does not mean we are replacing it with the resistance less wire. We can also solve it by solving each branch separately but it would be complicated. Make sure the condition is satisfied for the Wheatstone bridge.