Question

Find the equivalent resistance between the points A and B.

(A) $2\Omega$
(B) $4\Omega$
(C) $8\Omega$
(D) $16\Omega$

Answer 1

For solving this problem, we have to simplify this circuit by classifying each resistance according to the potential difference across it. Then, we need to redesign the given circuit using this classification.

Complete step by step solution:
We start by labelling each of the potential and resistance in the circuit as shown.

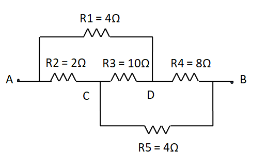
Now, we classify each resistance on the basis of the potential difference across it.

Resistance	Potential Difference
$R_1$ = $4\Omega$	VAD
$R_2$ = $2\Omega$	VAC
$R_3$ = $10\Omega$	VCD
$R_4$ = $8\Omega$	VBD
$R_5$ = $4\Omega$	VBC

Now, we again design the same circuit according to the above table.

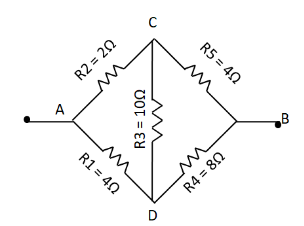
Here, we see that the circuit takes the shape of the Wheatstone bridge.
Now, we check the condition for Wheatstone bridge.
We know that for Wheatstone bridge condition to be valid in the above case, we should have
$\dfrac{{R_2}}{{R_1}} = \dfrac{{R_5}}{{R_4}}$
Checking the LHS and RHS, we have
$LHS = \dfrac{{R_2}}{{R_1}} = \dfrac{2}{4} = \dfrac{1}{2}$
$RHS = \dfrac{{R_5}}{{R_4}} = \dfrac{4}{8} = \dfrac{1}{2}$
Now, since both RHS and LHS are equal, the condition of Wheatstone is valid here.
Therefore, the resistance $R_3$ can be discarded out.
Thus, the circuit gets reduces to

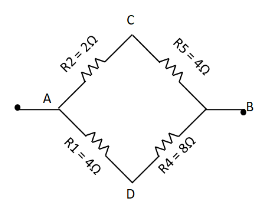
Here, we find that $R_2$ and $R_5$ are in series. Also, $R_1$ and $R_5$ are in series. As we know that the resistances in series get added. Therefore, the above circuit reduces to

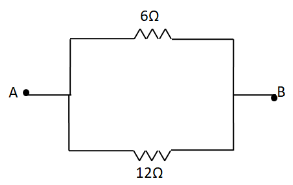
Now, the $6\Omega$ and $12\Omega$ resistances are in parallel. Therefore, the equivalent resistance, $R$ between A and B is given by
$\dfrac{1}{R} = \dfrac{1}{6} + \dfrac{1}{{12}}$
Taking the LCM, we have
$\dfrac{1}{R} = \dfrac{{2 + 1}}{{12}}$
$\dfrac{1}{R} = \dfrac{1}{4}$
Finally, taking the reciprocal we get the equivalent resistance
$R = 4\Omega$
Therefore, the equivalent resistance between the points A and B is equal to $4\Omega$
Hence, the correct answer is option B, $4\Omega$ .

Note:
We should not come to a direct conclusion that a given circuit is a Wheatstone bridge just by merely looking at the shape of the circuit. Always remember to check the required condition before applying this method.