Question

Find the equivalent resistance between points A and B.

A. $6\Omega$
B. $12\Omega$
C. $4\Omega$
D. $18\Omega$

Answer 1

The above circuit diagram represents a somewhat similar circuit as the Wheatstone’s Network or Wheatstone’s bridge, except for one thing that the sensitive galvanometer that should lie between PQ is now replaced by a resistance of $12\Omega$. Then if there is no current flow between PQ, the resistance connected between PQ will be infinite.

Formula Used:
If resistances ${R_a}$ and ${R_b}$ are connected in series, then the equivalent resistance is given by: ${R_{series}} = {R_a} + {R_b}$
If resistances ${R_a}$ and ${R_b}$ are connected in parallel, then the equivalent resistance is given by: $\dfrac{1}{{{R_{parallel}}}} = \dfrac{1}{{{R_a}}} + \dfrac{1}{{{R_b}}}$

Complete step by step answer:
The circuit diagram consists of four resistances of values $6\Omega$, $12\Omega$, $6\Omega$ and $3\Omega$ that form a quadrilateral of APBQ. Also, a resistance of $12\Omega$ is connected between PQ. This circuit diagram represents a Wheatstone’s bridge. But, here the resistance is used in place of a galvanometer.

Along loop AQB, there will be a certain point Q which has the potential that is equal to the potential at P along loop APB. When this condition is true, the network is said to be balanced. That means, the points P and Q are equipotential. If it is so, then the current flowing through PQ is zero. According to Ohm’s Law if the current is zero, then the resistance turns to be infinite. Infinite resistance is considered to be an open circuit. Therefore, the value of resistance will be nullified between PQ. And hence a simplified version of the above circuit diagram can be obtained.

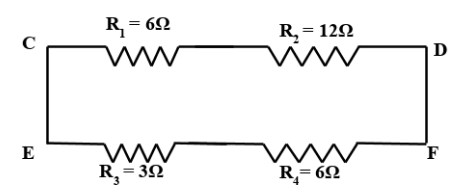
The resistances in both the segments CD and EF are in series. The equivalent resistance in individual segments can be given taking the sum of equivalent resistances.

\Rightarrow{R_{CD}} = 6\Omega + 12\Omega \\\ \Rightarrow{R_{CD}} = 18\Omega $$ $$\Rightarrow{R_{EF}} = {R_3} + {R_4} \\\ \Rightarrow{R_{EF}} = 3\Omega + 6\Omega \\\ \Rightarrow{R_{EF}} = 9\Omega $$ The resistances $${R_{CD}}$$ and $${R_{EF}}$$ are in a parallel combination. So the equivalent resistance between points A and B will be $$\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{{R_{CD}}}} + \dfrac{1}{{{R_{EF}}}} \\\ \Rightarrow\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{18\Omega }} + \dfrac{1}{{9\Omega }} \\\ \Rightarrow\dfrac{1}{{{R_{AB}}}} = \dfrac{3}{{18\Omega }} \\\ \Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{6\Omega }}$$ Therefore, $${R_{AB}} = 6\Omega $$ **Hence, option A is the correct answer.** **Note:** In the solution, it is said that the voltages at points P and Q are said to have equal potential. (This is the balanced condition). And then the current flowing through PQ is zero. This condition of equal voltages and zero current is considered (for an instance) to be in a situation where a source of e.m.f is connected between diagonally opposite sides A and B. And, a current flows from A to B. This balanced condition can also be verified by the equation $$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}}$$. Substituting the values, $$\dfrac{6}{{12}} = \dfrac{3}{6} \to \dfrac{1}{2} = \dfrac{1}{2}$$. Hence, the condition is verified. Therefore, the current through the arms PQ is zero.