Question

Find the equivalent resistance between A and B.

Answer 1

Take the branches in series and solve them and if any two resistance are in series we have to add them and after that they will come in parallel such that when the resistance are parallel we take the reciprocal of all the resistance and add them and finally we got our equivalent circuit.

Complete step by step solution:
Suppose that the circuit is complete from A and B with a battery and a current $I$ is flowing through B to A. Now, we see that the potential drop in point P is and the two branches with point P will have current $i$. And then the potential difference in point P and S is $V-iR$. Then these two points become the same potential point such that,$\Delta V=0$, it means no current will flow through branch QS. And the current flow in the branch PR will be $I-2i$.

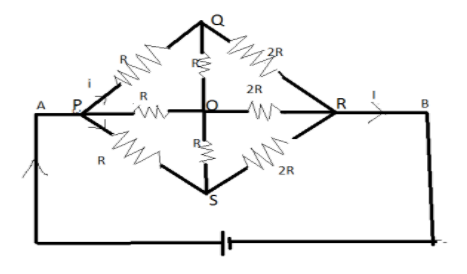
Now branch PQ and QR are both branches and are in series also branch RS and RP they also in the series. Hence, as R and 2R are in series then,
${{R}_{1}}=R+2R=3R$ eq. (1)

Similarly,
${{R}_{2}}=R+2R=3R$ eq. (2)

And also the branch PO and OR is in series thus,
${{R}_{3}}=R+R=2R$ eq. (3)

Now these three are in series that are $3R,3R$ and $2R$.

So here we have to use the formula through which we can find the equivalent resistance that is,
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$ eq. (4)
$\dfrac{1}{R}=\dfrac{1}{3R}+\dfrac{1}{3R}+\dfrac{1}{2R}$
$R=\dfrac{6R}{7}$

Note:
Here as in above one question may arise in our minds that the branch QO and OS are not having current and the branch is removed from the circuit since as we found above that the current gets distributed and the potential difference will be zero and hence those branches are negligible and no current passes through it.