Question

Find the equivalent resistance about any branch of the base of the square pyramid shown. Assume resistance of each branch is R.

A) $\dfrac{{7R}}{{15}}$
B) $\dfrac{{8R}}{{15}}$
C) $\dfrac{R}{2}$
D) ${\text{None of these}}$

Answer 1

This problem is completely based on simplifying the given circuit using logical reasoning like current direction and potential drop. Once simplified you need to see which connections are in series and which are in parallel. Then find the equivalent resistance accordingly.

Formulae used:
Equivalent resistance of n resistors connected in series connection is:
${R_{eq}} = {R_1} + \ldots + {R_i} + \ldots + {R_n}$.............(1)
Where,
${R_{eq}}$ denotes the equivalent resistance,
${R_i}$ denotes the resistance of the i number resistor.
Equivalent resistance of n resistors connected in parallel connection is:
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \ldots + \dfrac{1}{{{R_i}}} + \ldots + \dfrac{1}{{{R_n}}}$................(2)
Where,
${R_{eq}}$ denotes the equivalent resistance,
${R_i}$ denotes the resistance of the i number resistor.

Complete step by step answer:

Given: Resistance of each branch is the same as R.
To find: The equivalent resistance for any base branch of the square pyramid. Here, we’ll try to find equivalent resistance across CD.
Step 1
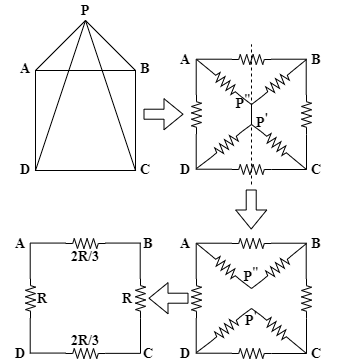
This square pyramid can simply be viewed as a square with four resistors at four sides and the center (P) connected with each vertex by a resistor. The second diagram (top right in the picture) is just this same picture except that the point P is broken into two points $P'$ and $P''$ which are connected by a resistance less wire.
Step 2
Now, notice in the top right diagram that as you try to find equivalent resistance across the CD side, the whole resistance setup is completely symmetric about the dashed line. Hence, voltage drop in both sides of the line will be exactly the same. So, everywhere on the line voltage will be exactly half of the total voltage dropped across the CD. Hence, $P'$ and $P''$ have the same potential and no current will flow between them. Omitting the connection between $P'$ and $P''$ you can draw the circuit as the third diagram (bottom left).
Step 3
Using eq.(2) equivalent resistance for two resistors connected in parallel can be written as:
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{{R_1} + {R_2}}}{{{R_1}{R_2}}} \\\ \therefore {R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \\\$....................(3)
Now, just focus on the $DP'C$ and $AP''B$ triangle parts of the circuit. In both cases 2 resistors are connected in series connection giving a resistance of 2R (using eq.(1)) and that 2R is in parallel with another R. So, using eq.(3) the equivalent resistance for this portion is:
${R'^{DP'C}}_{CD} = {R'^{AP''B}}_{AB} = \dfrac{{2R \times R}}{{2R + R}} = \dfrac{{2R}}{3}$
Step 4
Finally, the equivalent circuit becomes the circuit shown in fourth diagram (bottom right) where ${R'^{AP''B}}_{AB}$ is in series with two other resistors of resistance R . So, their equivalent resistance is:
${R'_{CD}}^{DABC} = {R'_{AB}}^{AP''B} + R + R = \dfrac{{2R}}{3} + 2R \\\ \therefore {R'_{CD}}^{DABC} = \dfrac{{8R}}{3} \\\$
Step 5
Now, ${R’_{CD}}^{DABC}$ and ${R'_{CD}}^{DP'C}$ are in parallel connection between CD. So, their equivalent resistance is:
$R_{CD} = \dfrac{{R'_{CD}}^{DABC} \times {R'_{CD}}^{DP'C}}{{R'_{CD}}^{DABC} + {R'_{CD}}^{DP'C}} = \dfrac{{\dfrac{{8R}}{3} \times \dfrac{{2R}}{3}}}{{\dfrac{{8R}}{3} + \dfrac{{2R}}{3}}} = \dfrac{{16{R^2}}}{9} \times \dfrac{3}{{10R}} \\\ \therefore {R_{CD}} = \dfrac{{8R}}{{15}} \\\$
Equivalent resistance about any branch is (B), $\dfrac{{8R}}{{15}}$.

Note: While simplifying the pyramid structure a student might get confused about where and how to break the circuit for simplification. Just follow current flow inside the circuit. Always remember that no current flows between two points having the same potential and you can cut that portion if no current flows through that part.