Question

Find the equivalent capacitance of the system given below:

(A) $\dfrac{{{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$
(B) $\dfrac{{{{2}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$
(C) $\dfrac{{{{3}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$
(D)$\dfrac{{{{4}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$

Answer 1

Hints to solve the problem above like.

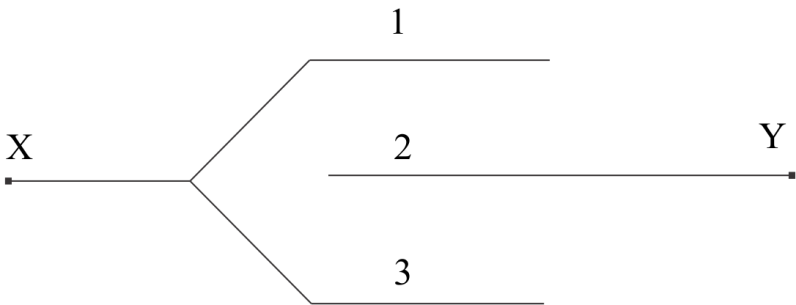
Consider the metallic plates $1,2$ and $3$ each of surface Area A, and are placed at a distance ‘d’ apart from each other and the two plates outer plates are connected each other as shown in the figure. Then the arrangement of Conductors behaves as a parallel Combination of two sub Capacitors has plate Area ‘A’ and the separation ‘d’. The Capacitance of the arrangement arrangement of the of the conductors is given by
${{C = }}\dfrac{{{{2}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$

Case-II

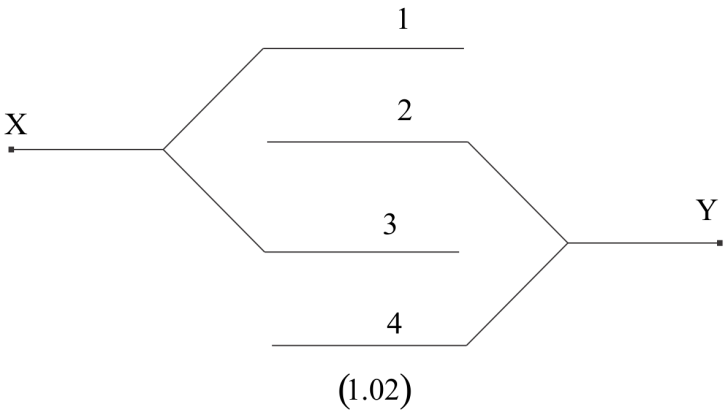
Now in the above figure we have four metallic plates $1,2,3$ and $4$,each surface area ‘A’ and are placed at a distance ‘d’ apart from each other and two alternative plates $\left( {2,4} \right)$ and the plates $\left( {1,3} \right)$ are connected to each other separately as shown in the figure $\left( {1.02} \right)$ . Then this arrangement shows the parallel Combination of three sub capacitors.
Each Sub Capacitor has plate area ’A’ and plate separation ‘d’. Then the Capacitance of the arrangement of the Conductors is
${{C = }}\dfrac{{{{3}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$

Complete step by step solution $: \to$ Step-I: The given diagram is

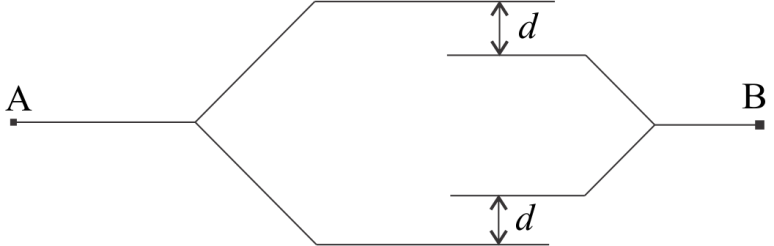
Suppose that the point A is connected to the positive terminal and B is connected to the negative terminal of the Battery.

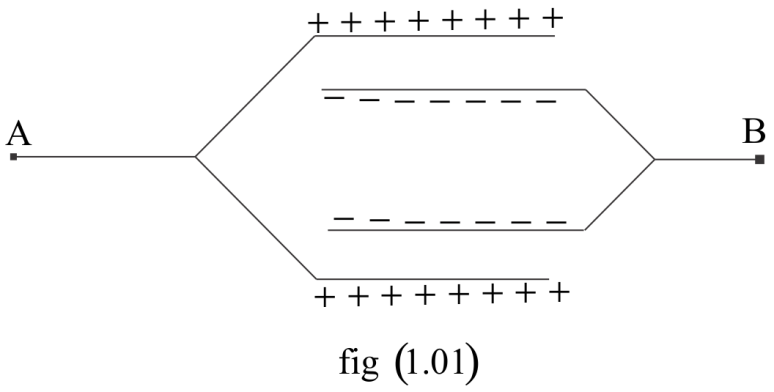
So now it is cleared from the Fig $1.01$ that it is the combination of two Capacitors in parallel.
Step $2$ Formula for the equivalent Capacitance in parallel.
${{{C}}_{{p}}} = {{{C}}_1} + {{{C}}_2}$
Both the Capacitor have same Capacitance $'{{c}}'$
So
${{{C}}_{{p}}} = {{C + C = 2C }} \to {{ 1}}$
Step $3$ formula for the Capacitance of parallel plate Capacitor
${{C = }}\dfrac{{{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$
Put value of ${{C}}$ in $1$
${{{C}}_{{{net}}}}{{ = }}\dfrac{{{{2}}{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$= net Capacitance between A & B

So option (B) is the correct answer.

Note: Electrical capacitance: It is the ability of a conductor to store the electric charge. The Capacitance of a parallel plate Capacitor is ${{C = }}\dfrac{{{{{\varepsilon }}_{{o}}}{{A}}}}{{{d}}}$. This formula is valid only if plates are held in vacuum or Air.