Question

Find the equivalent capacitance of the given circuit:

A $3C/2$
B $C/3$
C $3C$
D $C$

Answer 1

In this question, first the equivalent circuit needs to be drawn between the given terminal points to identify whether the given capacitors are in series or in parallel. Then apply the formula of the series combination or the parallel combination to calculate the equivalent capacitance.

Complete step by step solution:
In this question, the circuit of the capacitance is given which has three capacitors and we need to calculate the equivalent capacitance of the circuit.
The given circuit is,

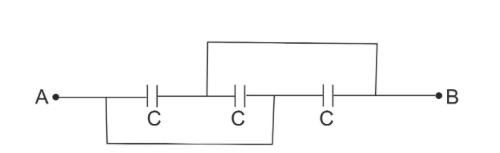
From the above diagram we can see that the potential difference between each capacitor is the same, so all the capacitors between point A and B are in parallel. Now, we consider the equivalent circuit of the capacitor as,

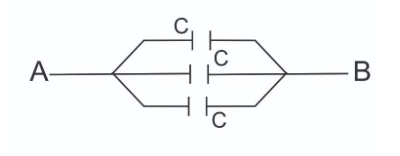
When capacitors are connected in parallel the equivalent capacitance, ${C_T}$ of the circuit is adequate to the sum of all the individual capacitors connected together.
By Parallel connection of Capacitor equation, we will calculate the equivalent capacitance of the capacitor as,
${C_T}{\text{ }} = {\text{ }}C{\text{ }} + {\text{ }}C{\text{ }} + \,{\text{ }}C$
After simplification, we get
$\therefore {C_T} = {\text{ }}3C$
Thus, the equivalent capacitance of the capacitor between the point A and B is $3C$.

Hence, the correct option is C.

Note: As we know that, if the capacitors are in parallel then the equivalent capacitance of the capacitor is the sum of the individual capacitors but if the capacitors are in series then the capacitance of the capacitor is determined by $\dfrac{1}{{{C_T}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$. Where, ${C_1},{C_2},{C_3}$ are the individual capacitance and in the parallel circuit the capacitor, the capacitance increases while, in the series combination, the capacitance of the circuit decreases.