Question
Question: Find the equivalent capacitance of the combination of capacitors between the points A and B. Also, f...
Find the equivalent capacitance of the combination of capacitors between the points A and B. Also, find a total charge that flows in the circuit when 100 V battery is connected between points A and B.
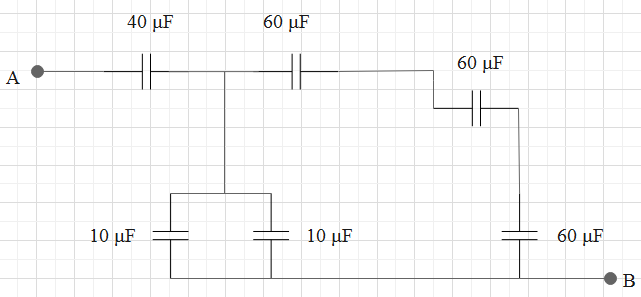
Solution
The problem is based on using the formulae of the capacitance of the capacitor. The series and the parallel capacitance of the capacitor should be calculated first. Then, the net capacitance should be multiplied with the given value of the voltage to obtain the value of the charge that flows through the circuit.
Formula used:
Q=CV
Complete step-by-step answer:
Consider the diagram representing component connections in a circuit.
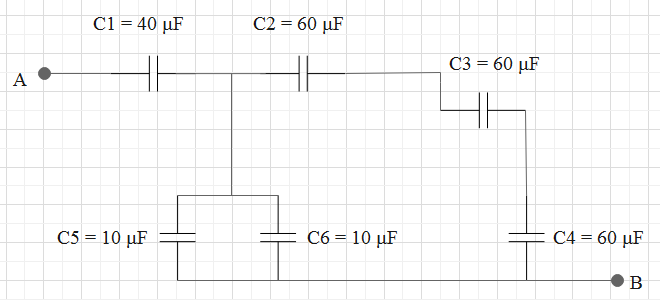
Considering the figure let us compute the capacitance of the circuit considering two capacitors at a time.
Let us begin the calculation.
Now consider the capacitors marked 5 and 6. So, these capacitors are in parallel. So, the equivalent capacitance is calculated as follows.
