Question
Question: Find the equivalent capacitance between X and Y is- (A). \(\dfrac{10}{3}\mu F\) (B). \(6\mu F\) ...
Find the equivalent capacitance between X and Y is-
(A). 310μF
(B). 6μF
(C). 8μF
(D). 26μF
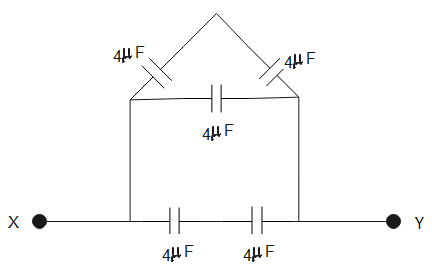
Solution
Capacitors can be connected together in different combinations; series combination and parallel combination. Solving the capacitors in series and parallel and replacing them by an equivalent capacitor, we can resolve and simply the capacitors’ combinations and hence calculate equivalent capacitance between given points.
Formulas used:
C1=C11+C21+C31+−−+Cn1
C′=C1+C2+C3+−−+Cn
Complete step by step solution:
Capacitance is defined as the ability of a body to store charge on it. Its SI unit is capacitance (C). It is given by-
C=VQ
Here, C is the capacitance
Q is the charge
V is the potential difference
The equivalent capacitance of capacitors connected in series is given by-
C1=C11+C21+C31+−−+Cn1 - (1)
The equivalent capacitance of capacitors connected in parallel is given by-
C′=C1+C2+C3+−−+Cn - (2)
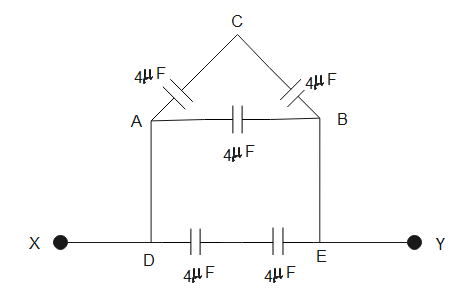
From the figure given above, the capacitors between AC and AB are in series and the capacitors in the arm DE are also in series.
The equivalent capacitance for ACB will be-
C11=41+41⇒C11=42∴C1=2μF
Similarly, equivalent capacitance between DE will be-
C21=41+41⇒C21=42∴C2=2μF
The figure given above can be simplified as-
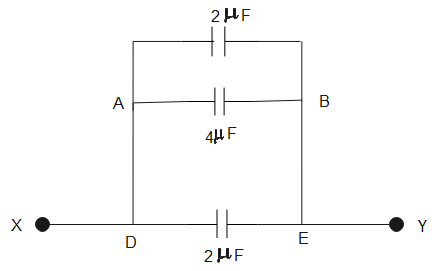
Since there are no elements between A and D and B and E, A coincides with D and B coincides with E. Similarly, D coincides with X and E coincides with Y.
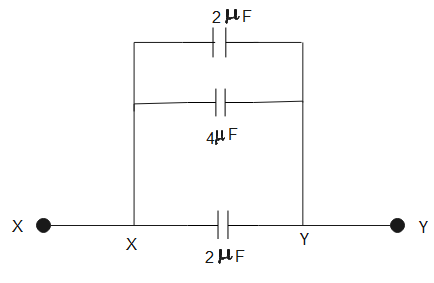
There are three capacitors connected in parallel between X and Y. The equivalent capacitance between X and Y will be-
C3=2+4+2⇒C3=8μF
The equivalent capacitance between X and Y is 8μF.
Therefore, the total capacitance between X and Y is 8μF. Hence, the correct option is (C).
Note: The capacitors are devices which store charge on it. The capacitance of a capacitor depends on the charge and potential difference. Combinations of capacitors are analogous to the combinations of resistors. The potential in a wire is the same and changes only after an element is introduced in it.
