Question

Find the equivalent capacitance between M and N

Answer 1

To solve this we need to use the formula for the equivalent capacitances for the capacitances arranged in series or in parallel combination. So first we need to find the equivalent between the last 2 capacitors in series, which is parallel to the $1\mu F$. The equivalent of these will be in series with the $2\mu F$ and parallel with $1\mu F$ again. Finally the whole equivalent capacitance will be in series with $2\mu F$.
Formula used: In this solution we will be using the following formula,
$\Rightarrow {C_{eq}} = {C_1} + {C_2} + {C_3} + ....$ where ${C_{eq}}$ is the equivalent capacitance when the capacitances are placed in parallel.
And $\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + ....$ where ${C_{eq}}$ is the equivalent capacitance when the capacitances are placed in a series circuit.

Complete step by step answer:
To find the equivalent capacitance first let us name the various points in the figure given above as,

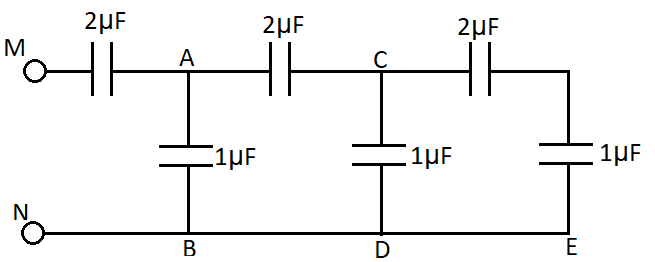
Now in between the points C and E we have 2 capacitances which are placed in series. So the equivalent capacitance between them will be given by the formula,
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + ....$
here we substitute ${C_1} = 2\mu F$ and ${C_2} = 1\mu F$
So substituting the values we get,
$\Rightarrow \dfrac{1}{{{C_{eq1}}}} = \dfrac{1}{2} + \dfrac{1}{1}$
Taking the LCM as 2 ,
$\Rightarrow \dfrac{1}{{{C_{eq1}}}} = \dfrac{{1 + 2}}{2}$
So we take the reciprocal on both the sides we get,
$\Rightarrow {C_{eq1}} = \dfrac{2}{3}\mu F$
Now between the points C and D ${C_{eq1}}$ and $1\mu F$ are in parallel. So the equivalent capacitance is given by the formula,
$\Rightarrow {C_{eq}} = {C_1} + {C_2} + {C_3} + ....$
So substituting ${C_1} = {C_{eq1}} = \dfrac{2}{3}\mu F$ and ${C_2} = 1\mu F$
Therefore, we get
$\Rightarrow {C_{eq2}} = \dfrac{2}{3} + 1$
Taking LCM as 3,
$\Rightarrow {C_{eq2}} = \dfrac{{2 + 3}}{3}$
Hence the value of the equivalent resistance between C and D is ${C_{eq2}} = \dfrac{5}{3}\mu F$
This capacitance is in series with $2\mu F$ between A and D.
Therefore again, ${C_1} = {C_{eq2}} = \dfrac{5}{3}\mu F$ and ${C_2} = 2\mu F$
So we get substituting in $\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + ....$
$\Rightarrow \dfrac{1}{{{C_{eq3}}}} = \dfrac{3}{5} + \dfrac{1}{2}$
Taking LCM as 10 we get,
$\Rightarrow \dfrac{1}{{{C_{eq3}}}} = \dfrac{{6 + 5}}{{10}}$
Taking the reciprocal we get,
$\Rightarrow {C_{eq3}} = \dfrac{{10}}{{11}}\mu F$
This capacitance is in parallel with $1\mu F$ between points A and B. So we get from the formula ${C_{eq}} = {C_1} + {C_2} + {C_3} + ....$,
$\Rightarrow {C_{eq4}} = \dfrac{{10}}{{11}} + 1$
Taking LCM as 11,
$\Rightarrow {C_{eq4}} = \dfrac{{10 + 11}}{{11}}$
Hence we get,
${\Rightarrow C_{eq4}} = \dfrac{{21}}{{11}}\mu F$
So between the points M and N the equivalent capacitance is given by the series of $\Rightarrow {C_{eq4}} = \dfrac{{21}}{{11}}\mu F$ and $2\mu F$. So substituting the values in the formula, $\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + ....$
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{{11}}{{21}} + \dfrac{1}{2}$
Taking LCM as 21
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{{22 + 21}}{{42}}$
So taking reciprocal we get
$\Rightarrow {C_{eq}} = \dfrac{{42}}{{43}}\mu F$
So this is the equivalent capacitance between the points M and N is ${C_{eq}} = \dfrac{{42}}{{43}}\mu F$.

Note:
When the capacitors are in parallel, then the total charge that is stored on all the plates is the sum of the charges that is stored on the individual plates. When the capacitors are in series, then the sum of the potential drop for each capacitor will give the total voltage across the circuit.