Question

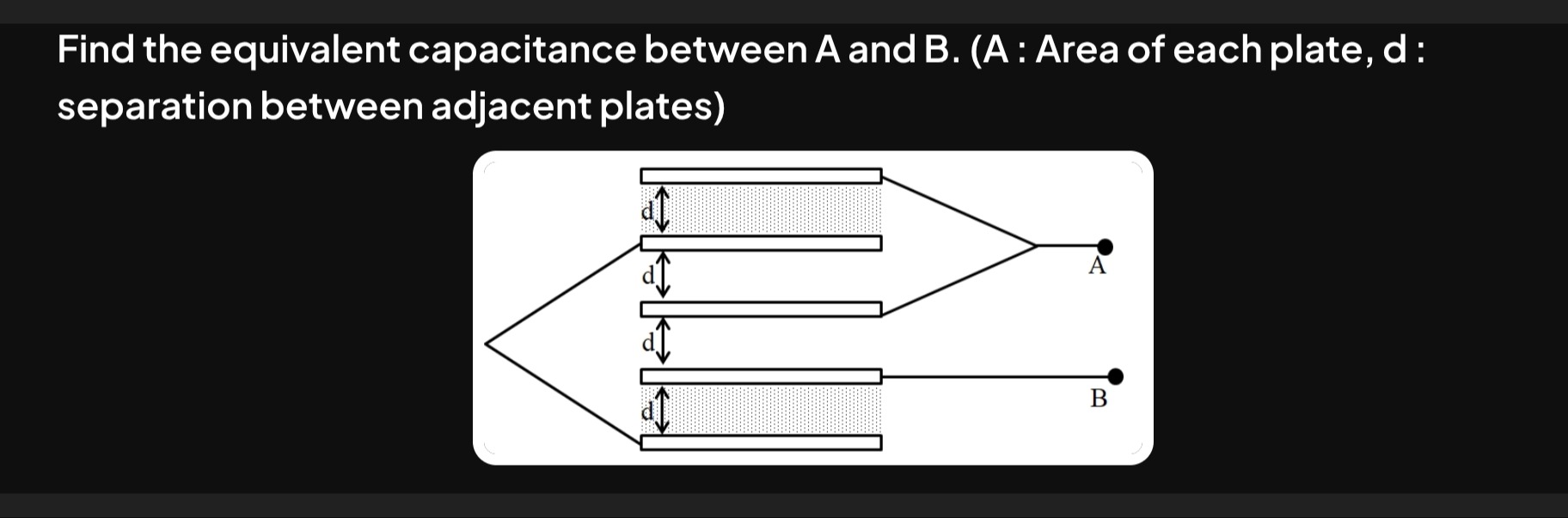
Find the equivalent capacitance between A and B. (A: Area of each plate, d : separation between adjacent plates)

Answer 1

3 \frac{\epsilon_0 A}{d}

Answer 2

To find the equivalent capacitance between points A and B, we first identify the potential of each plate and then determine how the individual capacitors formed by adjacent plates are connected.

Let the plates be numbered 1, 2, 3, 4, and 5 from top to bottom. The capacitance between any two adjacent plates is given by the formula for a parallel plate capacitor:

$C_0 = \frac{\epsilon_0 A}{d}$

where $\epsilon_0$ is the permittivity of free space, A is the area of each plate, and d is the separation between adjacent plates.

Now let's trace the connections:

• Plate 1 is connected to point A.
• Plate 2 is connected to point B.
• Plate 3 is connected to point A.
• Plate 4 is connected to point B.
• Plate 5 is connected to point B.

We can identify the individual capacitors formed by adjacent plates and their connections:

1. Capacitor $C_{12}$ (between Plate 1 and Plate 2):
   Plate 1 is at potential A, and Plate 2 is at potential B.
   Therefore, $C_{12}$ is connected between A and B. Its capacitance is $C_0$.

2. Capacitor $C_{23}$ (between Plate 2 and Plate 3):
   Plate 2 is at potential B, and Plate 3 is at potential A.
   Therefore, $C_{23}$ is connected between B and A (which is equivalent to being connected between A and B). Its capacitance is $C_0$.

3. Capacitor $C_{34}$ (between Plate 3 and Plate 4):
   Plate 3 is at potential A, and Plate 4 is at potential B.
   Therefore, $C_{34}$ is connected between A and B. Its capacitance is $C_0$.

4. Capacitor $C_{45}$ (between Plate 4 and Plate 5):
   Plate 4 is at potential B, and Plate 5 is at potential B.
   Since both plates are connected to the same terminal B, there is no potential difference across this pair of plates. Thus, this capacitor does not store charge and does not contribute to the equivalent capacitance between A and B.

All the contributing capacitors ($C_{12}$, $C_{23}$, and $C_{34}$) are connected in parallel between points A and B. For capacitors in parallel, the equivalent capacitance is the sum of individual capacitances:

$C_{eq} = C_{12} + C_{23} + C_{34}$
$C_{eq} = C_0 + C_0 + C_0$
$C_{eq} = 3C_0$

Substituting the value of $C_0$:

$C_{eq} = 3 \frac{\epsilon_0 A}{d}$