Question

Find the equivalent capacitance between A and B.

(A) $6C$
(B) $7C$
(C) $C$
(D) $5C$

Answer 1

Hint
To solve this question, we have to classify each capacitor according to its potential difference. Then, we need to redesign the given circuit using this classification.

Complete step by step answer
Let us label the centre point as O.

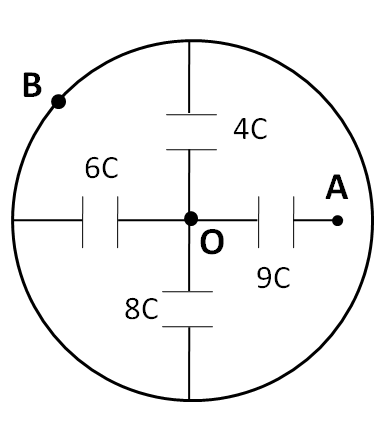
We know that a conducting wire has no drop. So, we label the potentials across the capacitors as

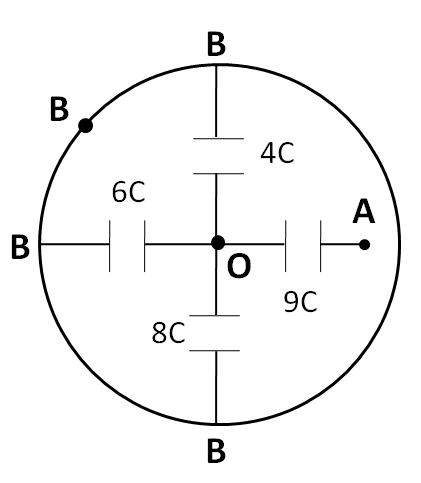
Now, we classify each capacitor according to the potential difference across it. The classification is shown in the table below.

Capacitance	Potential Difference
$4C$	VOB
$6C$	VOB
$8C$	VOB
$9C$	VOB

As can be seen from the above table, potential differences across the capacitances $4C$ , $6C$ , and $8C$ are the same, that is, VOB. So, these three capacitances are in parallel combination with each other. Hence, we redraw the given circuit as

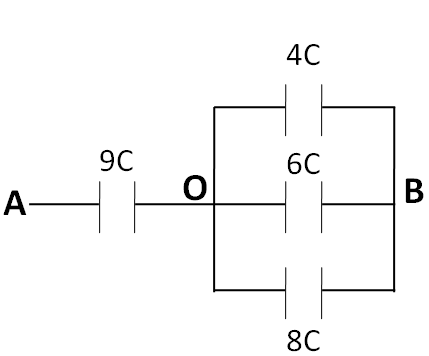
As the capacitances $4C$ , $6C$ , and $8C$ are in parallel combination, so the equivalent capacitance of these can be written as
$\Rightarrow {C_p} = 4C + 6C + 9C$
$\Rightarrow {C_p} = 18C$
So, the above circuit reduces to

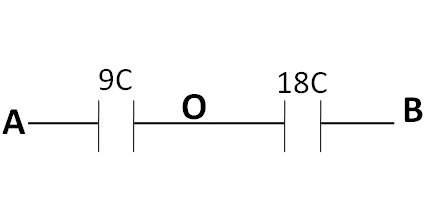
Since the capacitances $4C$ and $4C$ are in series, so finally, the equivalent capacitance between the points A and B is given by
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{9C}} + \dfrac{1}{{18C}}$
Taking the LCM
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{{2 + 1}}{{18C}}$
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{6C}}$
Finally, taking the reciprocal, we get
$\Rightarrow {C_{eq}} = 6C$
So the equivalent capacitance between A and B is $6C$
Hence, the correct answer is option A, $6C$ .

Note
While redesigning the original circuit using the voltage division method, do not make mistakes. Always set the capacitors having the end points connected to the same points parallel to each other first. Then, set other combinations in series keeping a check that the other combination should have a potential point common with the given combination.