Question

Find the equivalent capacitance across A and B.

(A). $\dfrac{35}{6}\mu F$
(B). $\dfrac{25}{6}\mu F$
(C). 15$\mu F$
(D). None of these.

Answer 1

First we need to disintegrate the circuit into many parts with respect to the capacitors in series or parallel, so that the calculation is made easy, after that we need to calculate all the series and parallel connections of the circuit which will give us the value of the equivalent capacitance in the circuit.

Complete step by step answer:

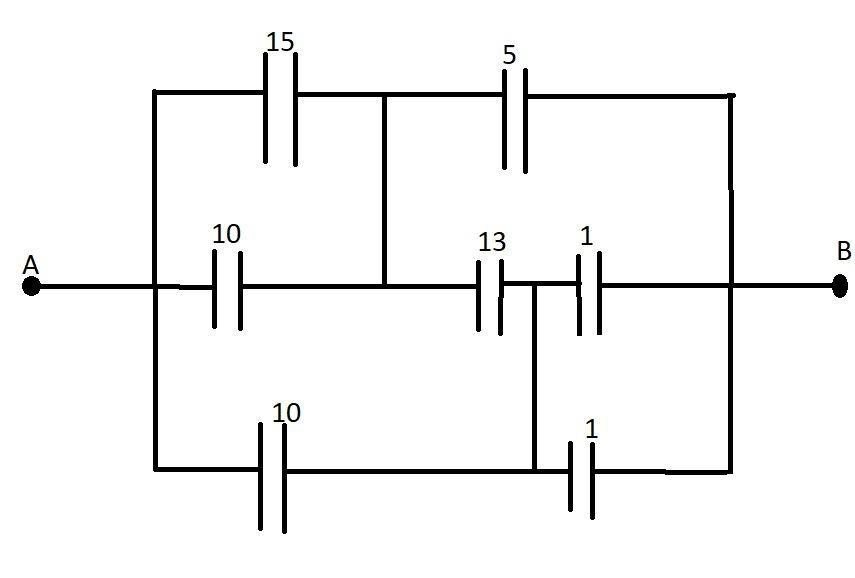
We see that the 15$\mu F$ , and the 10$\mu F$ capacitors are in parallel, so
C$_{eq1}$= (15+10)$\mu F$
C$_{eq1}$=25$\mu F$.

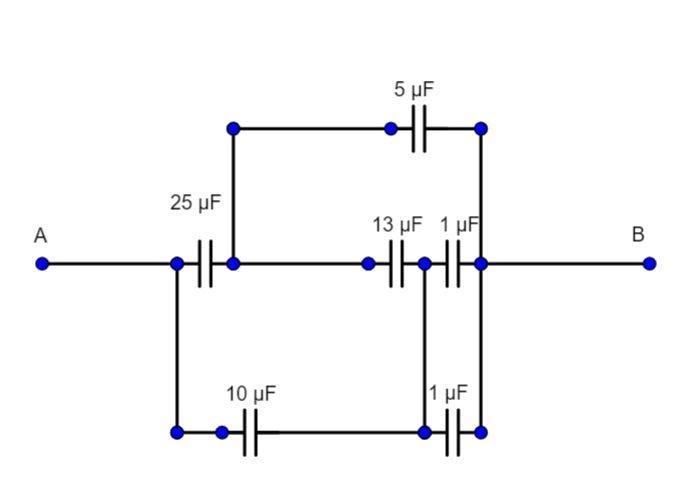
We further see that both the 1$\mu F$ capacitors are in parallel, so
C$_{eq2}$=(1+1) $\mu F$
C$_{eq2}$=2 $\mu F$.

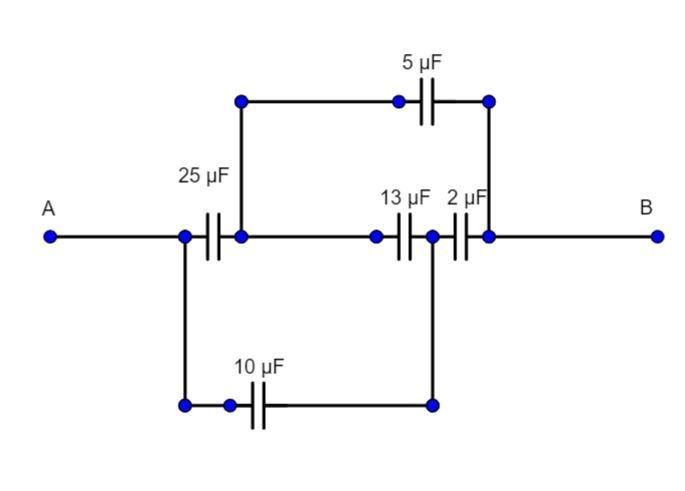
Now on comparing we see that C$_{eq2}$ and 13 $\mu F$ capacitors are in series,
So,
C$_{eq3}$=$\dfrac{13\times 2}{13+2}$
C$_{eq3}$=$1.733$

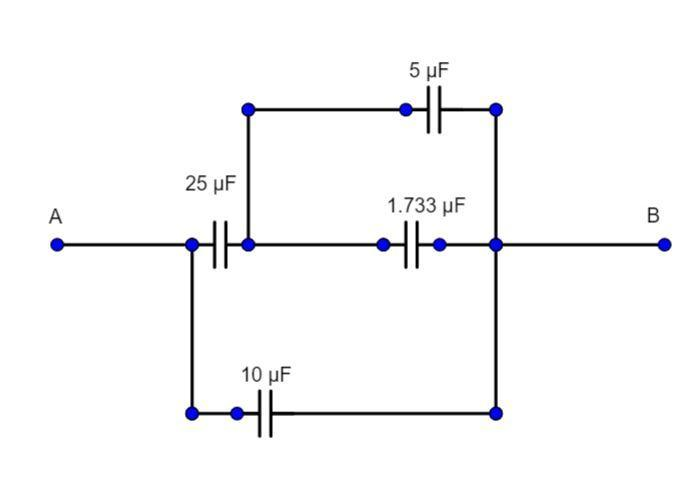
Now comparing C$_{eq3}$ and 5$\mu F$ capacitor that are in parallel,
C$_{eq4}$=$1.733$+5$\mu F$
C$_{eq4}$=$6.733$ $\mu F$

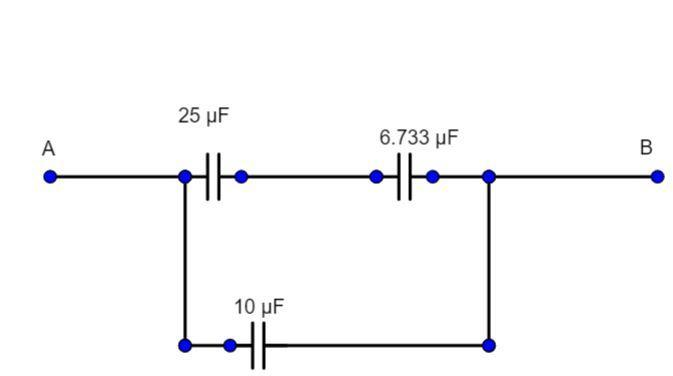
Now we see that,25$\mu F$and C$_{eq4}$ is in with each other which in turn us parallel to the 10 $\mu F$ capacitor that is below so,
$\dfrac{1}{C{}_{eq5}}=\dfrac{1}{6.733}+25$
$\dfrac{1}{C{}_{eq5}}=\dfrac{25+6.733}{168.32}\mu F$
$C{}_{eq5}=5.30\mu F$,
C$_{eq6}$ =$5.30+10$
C$_{eq6}$=$15.30\mu F$
Therefore the equivalent capacitance between the two is 15.30$\mu F$, which is option D (none of the above).

Additional Information:
A capacitor is a device which is used to store charge, it is usually made up of two conductors separated by an insulator.

Note:
When we calculate equivalent capacitance for a series circuit of capacitors we need to do a sum of both the capacitance simply, but when we find equivalent capacitance for a parallel circuit of capacitors we need to inverse each and every following term and find the result.