Solveeit Logo
Login

Question

Question: Find the equations to the altitudes of the triangle whose angular points are \(A\left( {2, - 2} \rig...

Find the equations to the altitudes of the triangle whose angular points are A(2,−2),B(1 ,1),C(−1,0)A\left( {2, - 2} \right),B\left( {1{\text{ }},1} \right),C\left( { - 1,0} \right) .

Explanation

Solution

Hint: In order to solve these type of question, we have to simply find out the slopes mm between two points i.e. AB,AC,BCAB,AC,BC using formula m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} and then convert them into slopes of the altitudes AD,BE,CFAD,BE,CF by using mAD=−1mBC{m_{AD}} = - \dfrac{1}{{{m_{BC}}}} , mBE=−1mAC{m_{BE}} = - \dfrac{1}{{{m_{AC}}}} , mCF=−1mAB{m_{CF}} = - \dfrac{1}{{{m_{AB}}}} after that substitute the value of mAD,mBE,mCF{m_{AD}},{m_{BE}},{m_{CF}} in equation for altitude between two points y−y1=m(x−x1)y - {y_1} = m\left( {x - {x_1}} \right) .

Complete step-by-step answer:

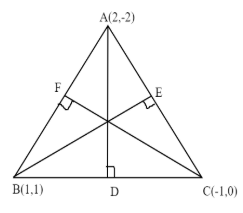
Given points are,
A(2,−2),B(1 ,1),C(−1,0)A\left( {2, - 2} \right),B\left( {1{\text{ }},1} \right),C\left( { - 1,0} \right)
Now we can find the slope of A(2,−2),B(1,1)A\left( {2, - 2} \right),B\left( {1,1} \right) by using the formula,
m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}
mAB= 1−(−2)1−2{m_{AB}} = {\text{ }}\dfrac{{1 - \left( { - 2} \right)}}{{1 - 2}}
Or mAB=−3{m_{AB}} = - 3
Therefore, using mCF=−1mAB{m_{CF}} = - \dfrac{1}{{{m_{AB}}}}
mCF= 13{m_{CF}} = {\text{ }}\dfrac{1}{3}
Using y−y1=m(x−x1)y - {y_1} = m\left( {x - {x_1}} \right)
y−0=13(x−(−1))y - 0 = \dfrac{1}{3}\left( {x - \left( { - 1} \right)} \right)
Or 3y=x+13y = x + 1
Or x−3y+1=0−−−−−−(1)x - 3y + 1 = 0 - - - - - - \left( 1 \right)
Similarly Slope of B(1 ,1),C(−1,0)B\left( {1{\text{ }},1} \right),C\left( { - 1,0} \right) is
mBC=0−1−1−1{m_{BC}} = \dfrac{{0 - 1}}{{ - 1 - 1}}
mBC=12{m_{BC}} = \dfrac{1}{2}
Therefore, using mAD=−1mBC{m_{AD}} = - \dfrac{1}{{{m_{BC}}}}
mAD=−2{m_{AD}} = - 2
Using y−y1=m(x−x1)y - {y_1} = m\left( {x - {x_1}} \right)
y−(−2)=(−2)(x−2)y - \left( { - 2} \right) = \left( { - 2} \right)\left( {x - 2} \right)
Or y+2=−2x+4y + 2 = - 2x + 4
Or y+2x−2=0−−−−(2)y + 2x - 2 = 0 - - - - \left( 2 \right)
Slope of A(2,−2),C(−1,0)A\left( {2, - 2} \right),C\left( { - 1,0} \right)
mAC=0−(−2)−1−2{m_{AC}} = \dfrac{{0 - \left( { - 2} \right)}}{{ - 1 - 2}}
Or mAC=−23{m_{AC}} = - \dfrac{2}{3}
Therefore, using mBE=−1mAC{m_{BE}} = - \dfrac{1}{{{m_{AC}}}}
mBE=32{m_{BE}} = \dfrac{3}{2}
Now, using y−y1=m(x−x1)y - {y_1} = m\left( {x - {x_1}} \right)
y−1=32(x−1)y - 1 = \dfrac{3}{2}\left( {x - 1} \right)
Or (y−1)2=3x−3\left( {y - 1} \right)2 = 3x - 3
Or 2y−2−3x−3=02y - 2 - 3x - 3 = 0
Or 2y−3x+1=0−−−−−(3)2y - 3x + 1 = 0 - - - - - \left( 3 \right)
Therefore, (1),(2),(3)\left( 1 \right),\left( 2 \right),\left( 3 \right) are the equations of CF , AD , and BE which are altitudes of the given triangle.
Note: Whenever we face these type of question the key concept is that firstly we have to find out the slopes of AB,AC,BCAB,AC,BC and the convert them into the slopes of altitudes AD,BE,CFAD,BE,CF and then put them in the equation of altitudes between two points and we will easily get our desired equations.