Question

Find the equations of the medians of a triangle, the co-ordinates of whose vertices are $\left( { - 1,\,6} \right),\,\left( { - 3,\, - 9} \right),\,\left( {5, - 8} \right)$

Answer 1

Hint : Firstly we will find the coordinates of point D,E and F. Further we will find slopes and equations of line AD,BE and CF also. Thereafter we will find the equation of the medians of a triangle.

Complete step-by-step answer :

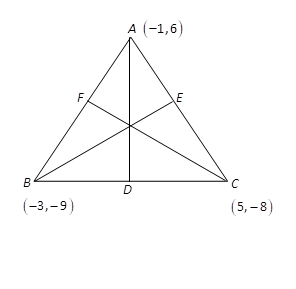
D is the midpoint of BC.
So $D\left( {\dfrac{{ - 3 + 5}}{2},\,\dfrac{{ - 9 + \left( { - 8} \right)}}{2}} \right)$
$\Rightarrow \,D\left( {1,\,\dfrac{{ - 17}}{2}} \right)$
Similarly, we can find points E and F
$E\left( {2,\, - 1} \right),\,F\left( { - 2,\,\dfrac{{ - 3}}{2}} \right)$
Equation of AD.
$y - {y_1} = m\left( {x - {x_1}} \right)$
Where $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Now for AD, we will consider $A\left( { - 1,\,6} \right),\,D\left( {1,\,\dfrac{{ - 11}}{2}} \right)$
$m = \dfrac{{\dfrac{{ - 17}}{2} - 6}}{{1 + 1}} = \dfrac{{ - 29}}{4}$
So equation of AD will be
$y - 6 = \dfrac{{ - 29}}{4}\left( {x + 1} \right)$
$\Rightarrow 4y - 24 = - 29x - 29$
$\Rightarrow 29x + 4y + 5 = 0$
Now slope of $BE = \dfrac{{ - 1 + 9}}{{2 + 3}} = \dfrac{8}{5}$
Equation of $BE \to y + 9 = \dfrac{8}{5}\left( {x + 3} \right)$
$\Rightarrow 5y + 45 = 8x + 24$
$\Rightarrow 8x - 5y - 21 = 0$
Slope of $CF \to \dfrac{{ - 8 + 2}}{{5 + 2}} = \dfrac{{ - 6}}{7}$
equation $\to y + 8 = \dfrac{{ - 6}}{7}\left( {x - 5} \right)$
$\Rightarrow 7y + 56 = - 6x + 30$
$\Rightarrow 6x + 7y + 86 = 0$

Note : Students remember that the Intersection point of medians is called centroid and centroid divide each median in 2:1. Median through a vertex of a triangle bisect the side joining other two vertices.