Question

Find the equation to the common chord of the two circles ${x^2} + {y^2} - 4x + 6y - 36 = 0$ and ${x^2} + {y^2} - 5x + 8y - 43 = 0$ and also find its length?

Answer 1

While finding the equation of the common chord of two given intersecting circles first we need to express each equation to its general form i.e., ${x^2}{\text{ }} + {\text{ }}{y^2}{\text{ }} + {\text{ }}2gx{\text{ }} + {\text{ }}2fy{\text{ }} + {\text{ }}c{\text{ }} = {\text{ }}0$ then subtract one equation of the circle from the other equation of the circle. We also know that the centre of the circle is (-g, -f). After using this, we will find the perpendicular distance from this point to the line. As we know, the line joining the two centres is always perpendicular to the common chord. Then by using Pythagoras theorem this half-length and after that multiply by two to get the final output.

Complete step by step answer:
Given that, The two circles are: ${C_1}:{x^2} + {y^2} - 4x + 6y - 36 = 0$ and ${C_2}:{x^2} + {y^2} - 5x + 8y - 43 = 0$. Let, the points of intersection of two circles are ${x_1},{y_1}$ and ${x_2},{y_2}$. Since both the points lie on both the circles, they will satisfy the equations of both the circles. Thus, the point $A({x_1},{y_1})$lies on both the given equations.
${x_1}^2 + {y_1}^2 - 4{x_1} + 6{y_1} - 36 = 0$ --- (i)
and
${x_1}^2 + {y_1}^2 - 5{x_1} + 8{y_1} - 43 = 0$ ---- (ii)
Subtract the equation (ii) from (i) and eliminate the terms ${x_1}^2$ and ${y_1}^2$ , we will get,
$\Rightarrow \left( { - 4{x_1} + 6{y_1} - 36} \right) - \left( { - 5{x_1} + 8{y_1} - 43} \right) = 0$
Removing the brackets, we will get,
$\Rightarrow - 4{x_1} + 6{y_1} - 36 + 5{x_1} - 8{y_1} + 43 = 0$
On evaluating this, we will get,
$\Rightarrow {x_1} - 2{y_1} + 7 = 0$

Again, for the point $B({x_2},{y_2})$lies on both the given equations.
Similarly for this point we will have,
$\Rightarrow {x_2} - 2{y_2} + 7 = 0$
These two equations show that the line $x - 2y + 7 = 0$ passes through both the points of intersection of the circles. Thus, the equation of the common chord of the two circles is $x - 2y + 7 = 0$. Compare equation of $C_1$, with the standard equation i.e. ${x^2} + {y^2} + 2gx + 2fy + c = 0$ we will get,
$2g = - 4$
$\Rightarrow g = - 2$
Also, $2f = 6$
$\Rightarrow f = 3$
Thus, the centre of the circle is point O =$( - g, - f) = (2, - 3)$.

From all the information, we will draw the figure below:

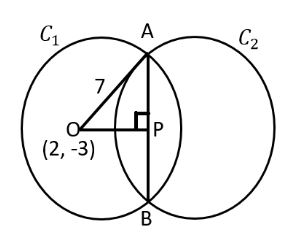
Next, the perpendicular distance from the point (2, -3) to the line is x-2y + 7 =0 is
$P = \left| {\dfrac{{2 - 2( - 3) + 7}}{{\sqrt {{1^2} + {{( - 2)}^2}} }}} \right|$
$\Rightarrow P = \left| {\dfrac{{2 + 6 + 7}}{{\sqrt {1 + 4} }}} \right|$
$\Rightarrow P = \left| {\dfrac{{15}}{{\sqrt 5 }}} \right|$

Next, line joining the two centres is always perpendicular to common chord and bisects the common chord, a right triangle will be formed of which the hypotenuse would be the radius of the circle (in this case it is 7) and the adjacent sides would be $\dfrac{{15}}{{\sqrt 5 }}$ and half length of the common chord. Now, by using Pythagoras theorem, the half-length would be:
$PA = \sqrt {{7^2} - {{\left( {\dfrac{{15}}{{\sqrt 5 }}} \right)}^2}}$
$\Rightarrow PA = \sqrt {49 - \dfrac{{225}}{5}}$
$\Rightarrow PA = \sqrt {\dfrac{{245 - 225}}{5}}$
$\Rightarrow PA = \sqrt {\dfrac{{20}}{5}}$
$\Rightarrow PA = \sqrt 4$
$\Rightarrow PA = 2$
Finally, the length of the common chord would be twice of this,
$2PA = 2(2) = 4$
Thus, the length of the chord is 4.

Hence, the equation of the common chord is $x - 2y + 7 = 0$ and its length is 4.

Note: The chord of a circle can be defined as the line segment joining any two points on the circumference of the circle. The chord of a circle is a line segment joining any two points on the circle. The chord of a circle which passes through the centre of the circle is called the diameter of the circle. The perpendicular bisector of any chord of a circle will pass through the centre of the circle.