Question

Find the equation to the circle: Whose radius is 3 and centre is (-1, 2)

Answer 1

Use the standard equation of the circle with the centre $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius of length ‘r’, which is given
$\Rightarrow {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$
Put $\left( {{x}_{1}},{{y}_{1}} \right)$ as $(-1,2)$ and r as ‘3’ to the above equation to get the required equation of the circle.

Complete step-by-step answer:
As we know the standard equation of a circle is given
$\Rightarrow {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}...............\left( i \right)$
where $\left( {{x}_{1}},{{y}_{1}} \right)$is the centre of the circle and ‘r’ is the radius of the circle and it is shown with the help of a diagram as

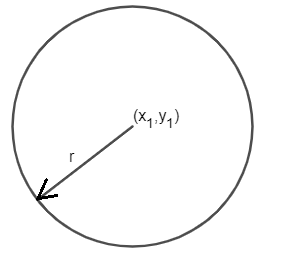
Now, coming to the question, we are given the centre of a circle as (-1, 2) and radius of it as 3 and hence, we need to determine the equation of the circle.
So, as equation (i) is representing the standard equation of a circle, with centre $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius ‘r’. Hence, we get
$\begin{aligned} & \left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,2 \right) \\\ & r=3 \\\ \end{aligned}$
So, we can put $\left( {{x}_{1}},{{y}_{1}} \right)$ as $\left( -1,2 \right)$ and r as 3 to the equation (i). So, we get the equation of the circle
$\begin{aligned} & \Rightarrow {{\left( x-\left( -1 \right) \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( 3 \right)}^{2}} \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=9................\left( ii \right) \\\ \end{aligned}$
Now, we can use the algebraic identity of ${{\left( a+b \right)}^{2}}$ and ${{\left( a-b \right)}^{2}}$ , which are given
$\begin{aligned} & \Rightarrow {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab...........\left( iii \right) \\\ & \Rightarrow {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab............\left( iv \right) \\\ \end{aligned}$
Hence, we can write equation (ii)
$\begin{aligned} & \Rightarrow {{x}^{2}}+1+2x+{{y}^{2}}+4-4y=9 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2x-4y+5-9=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2x-4y-4=0 \\\ \end{aligned}$
So, the equation of the circle with the given criteria is given
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2x-4y-4=0$

Note: Another approach to solving the question would be that we can use another standard equation of a circle given
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
Where $\left( -g,-f \right)$ is the centre of the circle and $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ is the radius of the circle.
So, we can put $\left( -g,-f \right)$ and$\left( -1,2 \right)$ to get ‘g’ and ‘f’ and equating $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ to 3(radius), we can get the value of ‘c’. So, it can be another approach.
One may prove the standard equation of the circle by the distance formula between two points. It is given
$\Rightarrow \text{Distance}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Suppose general point on a circle as $\left( x,y \right)$ and centre as $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius as ‘r’ and hence, use the above equation. So, get
${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$