Solveeit Logo
Login

Question

Question: Find the equation to that chord of the circle \( {x^2} + {y^2} = 81 \) which is bisected at the poin...

Find the equation to that chord of the circle x2+y2=81{x^2} + {y^2} = 81 which is bisected at the point (-2, 3), and its pole w.r.t the circle.

Explanation

Solution

Hint : In this particular question use the concept that chord is always a line, so assume general equation of line which is given as, y = mx + c and the chord bisected at point (-2, 3) so the line joining the center of the circle and this point makes a 90 degrees with the chord, so use slope concept that the multiplication of slopes when two lines are perpendicular to each other is -1, so use these concepts to reach the solution of the question.

Complete step-by-step answer :

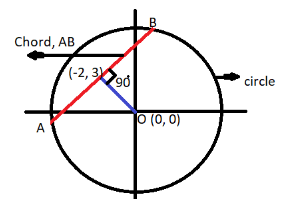
Given data:
Equation of the circle
x2+y2=81{x^2} + {y^2} = 81
Now as we know that the center of the above circle is (0, 0).
Now consider a chord AB as shown in the figure.
Let the equation of the chord be, y=m1x+cy = {m_1}x + c ............... (1)
Now it is given that this chord is bisected at point (-2, 3), so the line joining the center of the circle and this point makes a 90 degrees with the chord as shown in the figure.
Now when two points are given then the slope of that line passing through these points (x1,y1) and (x2,y2)\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right) are,
m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}
Let, (0, 0) = (x1,y1)\left( {{x_1},{y_1}} \right)
And, (-2, 3) = (x2,y2)\left( {{x_2},{y_2}} \right)
So the slope of the line passing through these points are, m=3−0−2−0=−32m = \dfrac{{3 - 0}}{{ - 2 - 0}} = - \dfrac{3}{2}
Now as we know that the multiplication of slopes when two lines are perpendicular to each other is -1.
Let the slope of the chord be m1{m_1}
⇒m.m1=−1\Rightarrow m.{m_1} = - 1
⇒m1=−1m\Rightarrow {m_1} = - \dfrac{1}{m}
⇒m1=23\Rightarrow {m_1} = \dfrac{2}{3}
Now rom equation (1) we have,
⇒y=m1x+c\Rightarrow y = {m_1}x + c
⇒y=23(x)+c\Rightarrow y = \dfrac{2}{3}\left( x \right) + c ................ (2)
Now this equation is passing fro point (-2, 3) so it satisfies the above equation so we have,
⇒3=23(−2)+c\Rightarrow 3 = \dfrac{2}{3}\left( { - 2} \right) + c
⇒3=−43+c\Rightarrow 3 = \dfrac{{ - 4}}{3} + c
⇒3+43=c\Rightarrow 3 + \dfrac{4}{3} = c
⇒c=133\Rightarrow c = \dfrac{{13}}{3}
Now from equation (2) we have,
⇒y=23(x)+133\Rightarrow y = \dfrac{2}{3}\left( x \right) + \dfrac{{13}}{3}
⇒3y=2x+13\Rightarrow 3y = 2x + 13
⇒2x−3y=−13\Rightarrow 2x - 3y = - 13 .................. (3)
So this is the required equation of the chord.
Now let the pole of this chord be (h, k)
So the equation of this line passing through that pole w.r.t circle is given as
⇒xh+yk=81\Rightarrow xh + yk = 81 .................. (4)
Now the equation (3) and (4) are similar.
Now as we know that the solution of the parallel lines (i.e. slope is same) or the same line (for example ax + by = c and lx + my = n) is given as al=bm=cn\dfrac{a}{l} = \dfrac{b}{m} = \dfrac{c}{n}
So the solution of equation (3) and (4) are
⇒h2=k−3=81−13\Rightarrow \dfrac{h}{2} = \dfrac{k}{{ - 3}} = \dfrac{{81}}{{ - 13}}
Now solve for h and k we have,
⇒h2=81−13\Rightarrow \dfrac{h}{2} = \dfrac{{81}}{{ - 13}}
⇒h=−16213\Rightarrow h = - \dfrac{{162}}{{13}}
And
⇒k−3=81−13\Rightarrow \dfrac{k}{{ - 3}} = \dfrac{{81}}{{ - 13}}
⇒k=24313\Rightarrow k = \dfrac{{243}}{{13}}
So the coordinates of the pole is (h,k)=(−16213,24313)\left( {h,k} \right) = \left( {\dfrac{{ - 162}}{{13}},\dfrac{{243}}{{13}}} \right)
So this is the required answer.

Note : Whenever we face such types of question the key concept we have to remember ids that always recall that the solution of the parallel lines (i.e. slope is same) or the same line (for example ax + by = c and lx + my = n) is given as al=bm=cn\dfrac{a}{l} = \dfrac{b}{m} = \dfrac{c}{n}, so first find out the equation of chord as above then equation passing through the pole w.r.t the circle as above then solve these two equations according to the above described formula we will get the required answer.