Question

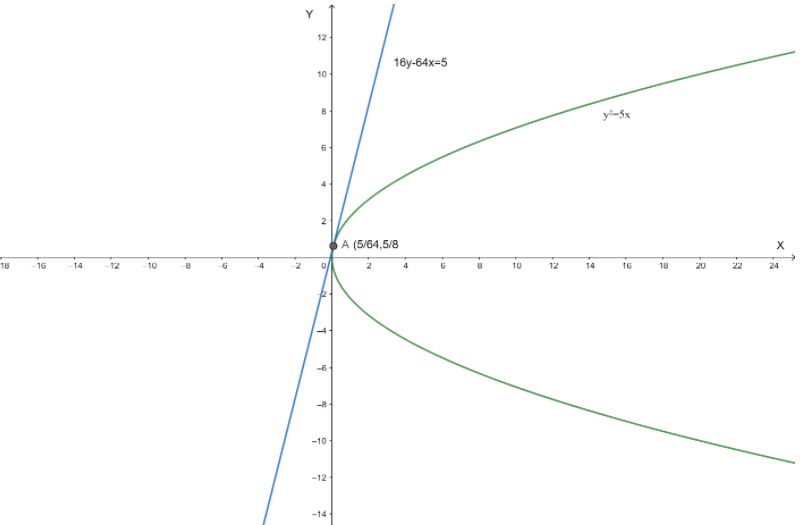
Find the equation of the tangent to the parabola ${y^2} = 5x$, that is parallel to $y = 4x + 1$ which meets the parabola at the coordinate $\left( {\dfrac{5}{{64}},\dfrac{5}{8}} \right)$.

Answer 1

First, we will find the slope of the tangent to the parabola by differentiating the equation of the given parabola. Then, we will equate the slope of the given line with that of the tangent because in the question it is given that they are parallel and we know parallel lines have the same slope. Then we will find the point of contact of the tangent and the parabola and at last we will find the equation of the tangent using the point slope form formula for the equation of the line.

Complete step by step solution:
Given parabola:
${y^2} = 5x$
Suppose the tangent touches the parabola at point $P\left( {x,y} \right)$.
Now we will find the slope of the tangent at point $P\left( {x,y} \right)$ by differentiating the parabola at point $P\left( {x,y} \right)$.
We have:
${y^2} = 5x$
Differentiating both sides we get;
$\Rightarrow \dfrac{{d{y^2}}}{{dx}} = \dfrac{{d\left( {5x} \right)}}{{dx}}$
On differentiation we get;
$\Rightarrow 2y\dfrac{{dy}}{{dx}} = 5$
We will shift $2y$ to the RHS.
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{5}{{2y}}$
Now this is the slope of the tangent at point $P\left( {x,y} \right)$.
Now we will find the slope of the line $y = 4x + 1$ by comparing it with the standard form of the line.
If: $y = mx + c$
Then the slope of this line is $m$.
For: $y = 4x + 1$
Slope $= 4$
Now in the question it is given that tangent and the line $y = 4x + 1$ are parallel. This means that both of them should have the same slope.
$\therefore \dfrac{5}{{2y}} = 4$
On shifting and rearranging we get;
$\Rightarrow 8y = 5$
$\Rightarrow y = \dfrac{5}{8}$
This is the ordinate of point $P\left( {x,y} \right)$.
To find the abscissa we will put the value of ordinate in the curve ${y^2} = 5x$.
$\therefore {\left( {\dfrac{5}{8}} \right)^2} = 5x$
$\Rightarrow 5x = \dfrac{{25}}{{64}}$
On simplification we get;
$\Rightarrow x = \dfrac{5}{{64}}$
So, the point of contact $P\left( {x,y} \right)$ is $P\left( {\dfrac{5}{{64}},\dfrac{5}{8}} \right)$.
Now we have the slope of the tangent and one of the points through which it passes. So, we can find its equation using point slope form which is given as;
If a line having slope $m$ passes through the points $\left( {{x_1},{y_1}} \right)$ then its equation is; $y - {y_1} = m\left( {x - {x_1}} \right)$.
The tangent passes through $P\left( {\dfrac{5}{{64}},\dfrac{5}{8}} \right)$ and it has the slope $= 4$.
So, its equation is:
$y - \dfrac{5}{8} = 4\left( {x - \dfrac{5}{{64}}} \right)$
Taking the LCM and solving we get;
$\Rightarrow \dfrac{{8y - 5}}{8} = 4\left( {\dfrac{{64x - 5}}{{64}}} \right)$
Multiplying both sides by $8$ we get:
$\Rightarrow 8y - 5 = 4\left( {\dfrac{{64x - 5}}{8}} \right)$
$\Rightarrow 8y - 5 = \dfrac{{64x - 5}}{2}$
Cross multiplying $2$ we get;
$\Rightarrow 2\left( {8y - 5} \right) = 64x - 5$
Expanding the bracket.
$\Rightarrow 16y - 10 = 64x - 5$
Shifting the terms, we get;
$\Rightarrow 16y - 64x = 5$

Note: One important point to note is that the slope of a curve depends on the location of the point where the slope is calculated. But in the case of a straight line that is the linear equation the slope is constant and hence is same for all the points on that line.