Question

Find the equation of the tangent to the parabola ${{x}^{2}}=4y$ with gradient unity. Also find the area enclosed by the curve, the tangent line and
(i) the $x$ axis.

Answer 1

Hint: Try to imagine what the graph of $y=\dfrac{{{x}^{2}}}{4}$ would look like. This is also a quadratic in $x$. So, it would most probably look like a bowl touching the $x$ axis at the origin, since the value of $y$ increases faster than the value of $x$. Next, write the general equation of the tangent to this curve which is $y=mx-a{{m}^{2}}$, and find the point where it touches the parabola. You will then get the limits of the integral you have to integrate.

Complete Step-by-Step Solution:
For a parabola of the general formula ${{x}^{2}}=4ay$, the tangent to any point lying on the parabola can be written as : $y=mx-a{{m}^{2}}$, where m is the slope of the tangent, and is thus, variable.
Comparing the parabola given to us in the question, to the general formula, we get :
$\begin{aligned} & 4ay=4y \\\ & \Rightarrow 4a=4 \\\ & \Rightarrow a=1 \\\ \end{aligned}$
Thus, the equation of a tangent to this parabola is : $\begin{aligned} & y=mx-a{{m}^{2}} \\\ & \Rightarrow y=mx-{{m}^{2}} \\\ \end{aligned}$, where $m$ is the slope and is variable.
It is given to us in the question that the gradient of this tangent should be unity, and hence, the slope of the tangent should be equal to 1, or $m=1$. Substituting for $m$ in the equation of the general tangent, we get :
$\begin{aligned} & y=mx-{{m}^{2}} \\\ & \Rightarrow y=x-1 \\\ & \Rightarrow x-y=1 \\\ \end{aligned}$
Let’s call this equation as equation (1).
Now, let’s analyse the parabola given to us. It looks like a quadratic, where the coefficient of ${{x}^{2}}$ is positive. Hence, we know that the graph of this parabola will be concave upward. Since we can’t see any constant term in this equation, we can safely conclude that the graph passes through the origin definitely.
Satisfying the equation with the origin also confirms our assumption. However, since $\begin{aligned} & {{x}^{2}}=4y \\\ & \Rightarrow y=\dfrac{{{x}^{2}}}{4} \\\ \end{aligned}$, we know that $y$ can be 0 at only one value, since both the roots of this equation will be 0 only.
Thus, we can now picture the graph better. It looks like a bowl, and touches the origin.
Now, let’s find the point where the tangent touches this parabola.
Substituting for $y$, in terms of $x$ from (1), in the equation of the parabola, we get :
$\begin{aligned} & {{x}^{2}}=4y \\\ & \Rightarrow {{x}^{2}}=4(x-1) \\\ & \Rightarrow {{x}^{2}}=4x-4 \\\ & \Rightarrow {{x}^{2}}-4x+4=0 \\\ & \Rightarrow {{x}^{2}}-2x-2x+4=0 \\\ & \Rightarrow x(x-2)-2(x-2)=0 \\\ & \Rightarrow {{(x-2)}^{2}}=0 \\\ & \Rightarrow x=2 \\\ & y=x-1 \\\ & \Rightarrow y=2-1=1 \\\ & (x,y)=(2,1) \\\ \end{aligned}$
Therefore, the point where the tangent touches the parabola is (2,1).
Now let’s imagine the area being asked for. We need to find the area enclosed between the tangent, the parabola, and the $x$ axis. Keep in mind that the parabola touches the $x$ axis at the origin already.
Therefore, we can interpret the area being asked for in the following manner : it is the difference of the area enclosed by the parabola from $x=0$ to $x=2$and the area enclosed by the line in the same interval.
In general, if $f(x)$ is a curve lying above $g(x)$ on the graph, then the area enclosed by the $x$ axis, $f(x)$ and $g(x)$ in the interval (a,b) = $|\int\limits_{a}^{b}{f(x)-g(x)dx|}=|\int\limits_{a}^{b}{f(x)dx-\int\limits_{a}^{b}{g(x)dx}}|$
Here, imagining will make us realise that the parabola lies above the tangent in the graph, and hence $f(x)$=parabola and $g(x)$=tangent with gradient unity, and the interval = (0,2).
Here’s a diagram to help you imagine the figure.

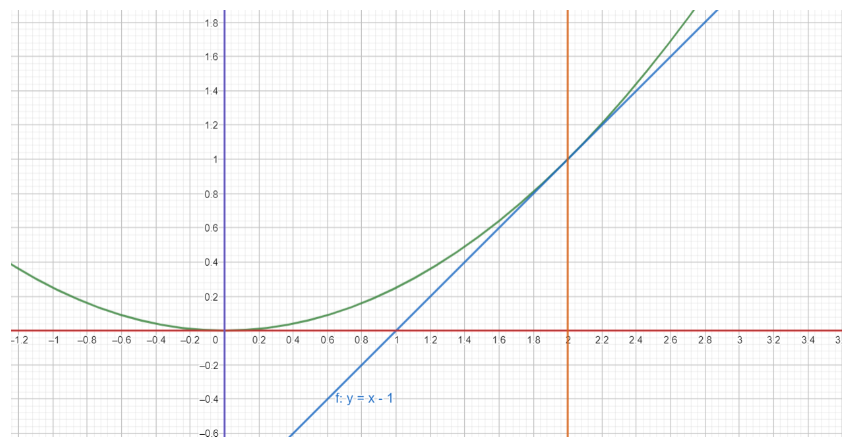
Hence, the required area = $\begin{aligned} & |\int\limits_{a}^{b}{f(x)dx}-\int\limits_{a}^{b}{g(x)dx|=|\int\limits_{0}^{2}{\dfrac{{{x}^{2}}}{4}dx-\int\limits_{0}^{2}{(x-1)dx|}}} \\\ & =|[\dfrac{{{x}^{3}}}{12}-\dfrac{{{x}^{2}}}{2}+x]_{0}^{2}|=|(\dfrac{8}{12}-\dfrac{4}{2}+2)-(0-0+0)| \\\ & =|\dfrac{2}{3}-2+2|=\dfrac{2}{3} \\\ \end{aligned}$
Therefore, we have our required area, $\dfrac{2}{3}$.
Then the required area = $\dfrac{2}{3}$.

Note: Hence, from the diagram, you can clearly see that the tangent touches the parabola at (2,1), and the area asked for is indeed the difference of the area enclosed by the parabola and the tangent, in the interval (0,2).