Question

Find the equation of the tangent at the point (4, 3) on the circle ${x^2} + {y^2} = 25$.

Answer 1

Hint: We had to only use the identity to find the equation of tangent that is T = 0, where T = $x\left( {{x_1} + g} \right) + y\left( {{y_1} + f} \right) + g{x_1} + f{y_1} + c = 0$ for the standard equation of circle i.e. ${x^2} + {y^2} + 2gx + 2fy + c = 0$.

Complete step-by-step answer:

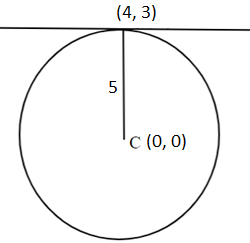
As we know that the standard equation of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$.
Now if we are given the point of contact of tangent to this circle as $\left( {{x_1},{y_1}} \right)$. Then to find the equation of tangent we will use the formula T = 0.
Now to find the value of T, we had to do only some changes in the equation of the circle.
Replace ${x^2}$ with $x{x_1}$
Replace ${y^2}$ with $y{y_1}$
Replace $x$ with $\dfrac{{\left( {x + {x_1}} \right)}}{2}$
Replace $y$ with $\dfrac{{\left( {y + {y_1}} \right)}}{2}$
And the constant will remain the same.
So, the equation of tangent to the standard equation of circle will be,

$$x{x_1} + y{y_1} + 2g\dfrac{{\left( {x + {x_1}} \right)}}{2} + 2f\dfrac{{\left( {y + {y_1}} \right)}}{2} + c = 0 \\\ x\left( {{x_1} + g} \right) + y\left( {{y_1} + f} \right) + g{x_1} + f{y_1} + c = 0 \\\$$

Now the given equation of circle is ${x^2} + {y^2} - 25 = 0$
So, this equation has only ${x^2}$, ${y^2}$ and constant terms.
And the point is given as (4, 3)
So, applying T = 0 to find the equation of tangent to the circle at point (4, 3). We get,
$4x + 3y - 25 = 0$
Hence, the equation of the tangent at the point (4, 3) on the circle ${x^2} + {y^2} = 25$ will be $4x + 3y - 25 = 0$.

Note:- Whenever we come up with this type of problem when we are given with the point of contact and the equation of circle then there is another method also to find the equation of tangent that is first we can find the coordinates of the centre of the circle by comparing the given equation with the standard equation of the circle and after that find the slope of the radius of the circle using two points (centre and contact point) and after that as we know that the tangent is perpendicular to the line joining centre and the point of contact. So, we can use the property of ${m_1}{m_2} = - 1$ to find the slope of the tangent. After that we can easily find the equation of tangent using point slope form that is $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$, where $\left( {{x_1},{y_1}} \right)$ will be the given point and m is the slope of the tangent.