Question

Find the equation of the tangent and normal to ellipse $16{{x}^{2}}+25{{y}^{2}}=400$ at the point where the value of $\tan \theta =\dfrac{1}{\sqrt{3}}$? Here $\theta$ is the eccentric angle of the ellipse.

Answer 1

We start solving the problem by converting the given equation of ellipse into its standard form and recalling the definition of eccentric angle. We calculate the value of the parametric angle $\theta$ using $\tan \theta =\dfrac{1}{\sqrt{3}}$. Once we find the value of parametric angle $\theta$, we substitute this in the standard equations of tangent and normal to get the required equations.

Complete step by step answer:
Given that we have equation of the ellipse as $16{{x}^{2}}+25{{y}^{2}}=400$. We need to find the equation of tangent and normal to the ellipse where the tangent of the eccentric angle is given as $\dfrac{1}{\sqrt{3}}$.
We know that the standard form of the parabola is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Let us convert the given equation $16{{x}^{2}}+25{{y}^{2}}=400$ in the standard form.
$\Rightarrow \dfrac{16{{x}^{2}}+25{{y}^{2}}}{400}=\dfrac{400}{400}$.
$\Rightarrow \dfrac{16{{x}^{2}}}{400}+\dfrac{25{{y}^{2}}}{400}=\dfrac{400}{400}$.
$\Rightarrow \dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1$.
$\Rightarrow \dfrac{{{x}^{2}}}{{{5}^{2}}}+\dfrac{{{y}^{2}}}{{{4}^{2}}}=1$.
We have got the values of a and b as 5 and 4.
We know that the parametric equation for the point in a ellipse is given as $\left( a\cos \theta ,b\sin \theta \right)$.
Let us draw the given information to get a better view.

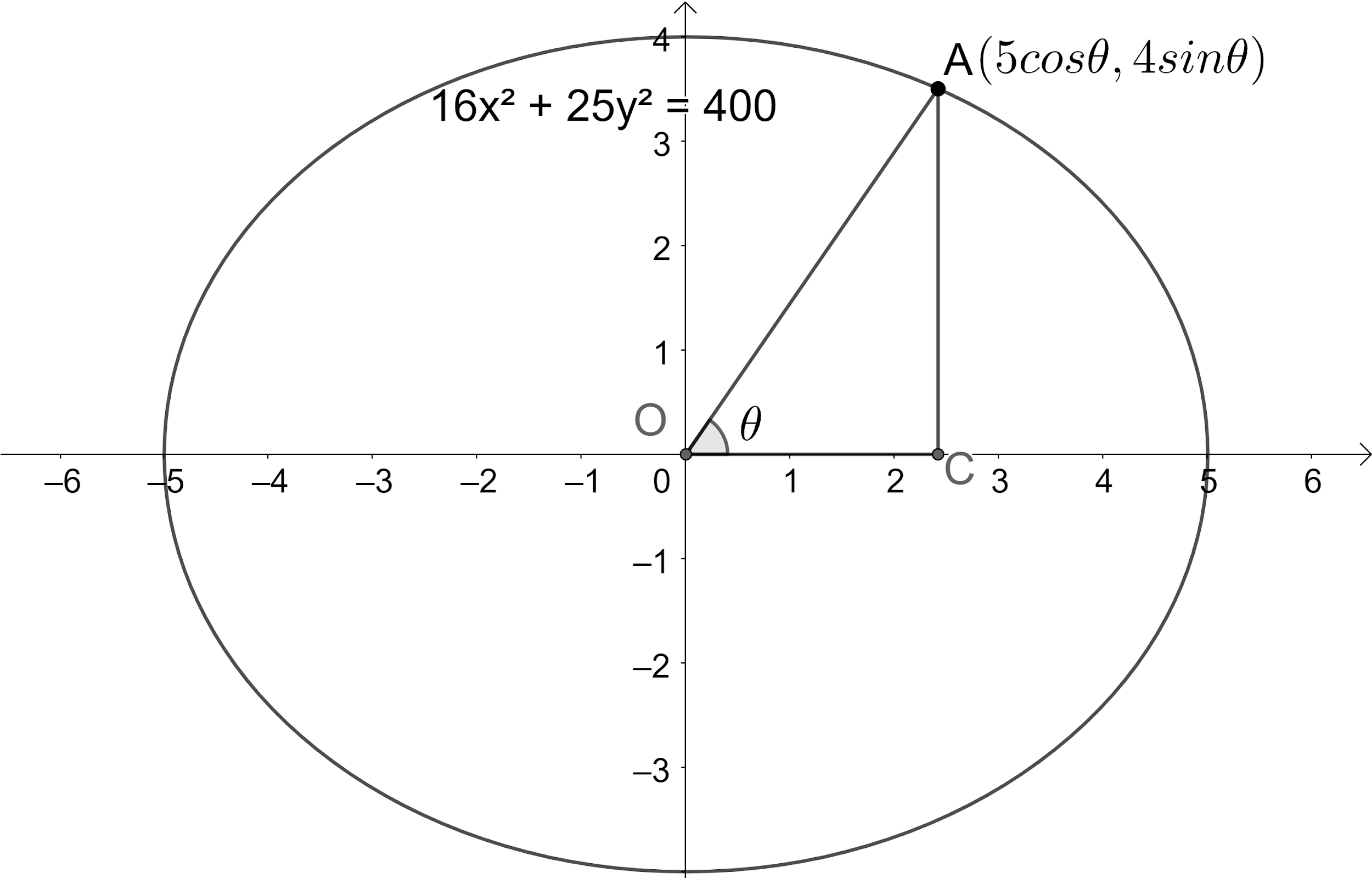
Let us find the value of $\theta$. We have $\tan \theta =\dfrac{1}{\sqrt{3}}$.
$\Rightarrow \tan \theta =\tan \left( {{30}^{o}} \right)$.
$\Rightarrow \theta ={{30}^{o}}$---(1).
We got the parametric angle for the point on ellipse as ${{30}^{o}}$.
We know that the equation of the tangent at the point on ellipse with parametric angle $\theta$ is $\dfrac{x}{a}\cos \theta +\dfrac{y}{b}\sin \theta =1$.
So, the equation of tangent of the ellipse $16{{x}^{2}}+25{{y}^{2}}=400$ is $\dfrac{x}{5}\cos \left( {{30}^{o}} \right)+\dfrac{y}{4}\sin \left( {{30}^{o}} \right)=1$.
$\Rightarrow \dfrac{x}{5}\times \dfrac{\sqrt{3}}{2}+\dfrac{y}{4}\times \dfrac{1}{2}=1$.
$\Rightarrow \dfrac{\sqrt{3}x}{10}+\dfrac{y}{8}=1$.
$\Rightarrow \dfrac{4\sqrt{3}x+5y}{40}=1$.
$\Rightarrow 4\sqrt{3}x+5y=40$.
We have got the equation of the tangent as $4\sqrt{3}x+5y=40$.
We know that the equation of the normal at the point on ellipse with parametric angle $\theta$ is $\dfrac{ax}{{{a}^{2}}-{{b}^{2}}}\sec \theta -\dfrac{by}{{{a}^{2}}-{{b}^{2}}}\operatorname{cosec}\theta =1$.
So, the equation of normal of the ellipse $16{{x}^{2}}+25{{y}^{2}}=400$ is $\dfrac{5x}{25-16}\sec \left( {{30}^{o}} \right)-\dfrac{4y}{25-16}\operatorname{cosec}\left( {{30}^{o}} \right)=1$.
$\Rightarrow \dfrac{5x}{9}\times \dfrac{2}{\sqrt{3}}-\dfrac{4y}{9}\times 2=1$.
$\Rightarrow \dfrac{10x}{9\sqrt{3}}-\dfrac{8y}{9}=1$.
$\Rightarrow \dfrac{10x-8\sqrt{3}y}{9\sqrt{3}}=1$.
$\Rightarrow 10x-8\sqrt{3}y=9\sqrt{3}$.
We have got the equation of the normal as $10x-8\sqrt{3}y=9\sqrt{3}$.

∴ The equations of tangent and normal of the ellipse $16{{x}^{2}}+25{{y}^{2}}=400$ are $4\sqrt{3}x+5y=40$ and $10x-8\sqrt{3}y=9\sqrt{3}$.

Note: We get the same value for the x coordinates of both points on the auxiliary circle and ellipse for a given parametric angle. We can also find the equations of the tangent and normal by first finding the point on the ellipse and finding the slopes of tangent and normal. We should know that the tangent and normal are perpendicular to each other. Similarly, we expect problems to find the length of the latus rectum, eccentricity of the ellipse.