Question

Find the equation of the system of coaxial circles that are tangent at $\left( {\sqrt 2 ,4} \right)$ to the locus of the point of intersection of two mutually perpendicular tangents to the circle ${x^2} + {y^2} = 9$

Answer 1

To solve this question, we have to remember that a system of circles is coaxial if every pair of circles from the system have the same radical axis. The locus of points with equal powers with respect to the two circles is called the radical axis of two circles. The radical axis of two circles ${x^2} + {y^2} + 2{g_1}x + 2{f_1}y + {c_1} = 0$ and ${x^2} + {y^2} + 2{g_2}x + 2{f_2}y + {c_2} = 0$ is clearly the straight line $2\left( {{g_1} - {g_2}} \right)x + 2\left( {{f_1} - {f_2}} \right)y + \left( {{c_1} - {c_2}} \right) = 0$

Complete step-by-step answer:
Given that,
Equation of circle = ${x^2} + {y^2} = 9$ ….. (i)
Comparing this with general equation of circle, ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, we will get
$\Rightarrow \left( {h,k} \right) = \left( {0,0} \right)$ and $r = 3$
System of coaxial circles is tangent at $\left( {\sqrt 2 ,4} \right)$ to the locus of the point of intersection of two mutually perpendicular tangents to the circle.
We have to find out the equation of this system of coaxial circles.
First, we will find the locus of point of intersection of two mutually perpendicular tangents to the circle ${x^2} + {y^2} = 9$

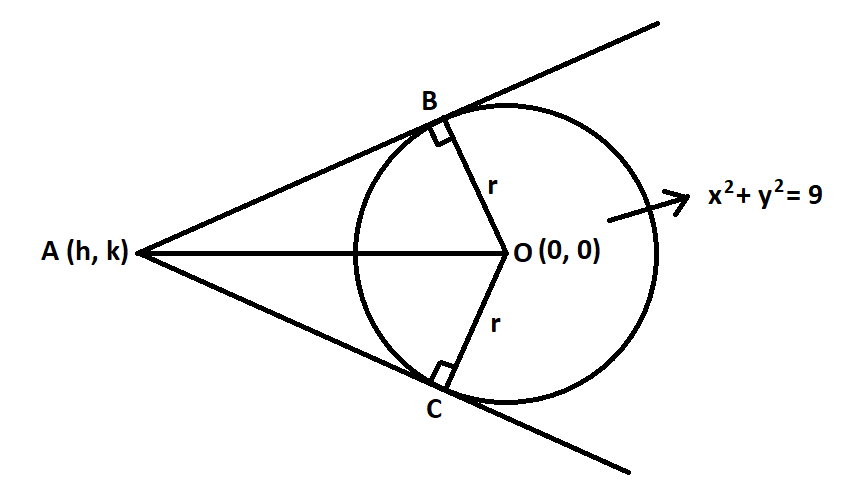
Let $A\left( {h,k} \right)$ be point of intersection of tangents of circle ${x^2} + {y^2} = 9$
So,
In $\vartriangle OAB$ and $\vartriangle OAC$,
$\Rightarrow \angle OBA = \angle OCA = {90^0}$ [radius is perpendicular to tangent]
$\Rightarrow OA = OA$ [common side]
$\Rightarrow OB = OC = r$ [radius of circle]
Then,
$\Rightarrow \vartriangle OAB \cong \vartriangle OAC$ [by SAS rule]
Hence,
$\Rightarrow \angle OAB = \angle OAC = {45^0}$ [by C.P.C.T.] $\therefore$ both tangents are mutually perpendicular, i.e. $\angle BAC = {90^0}$
From equation (i),
We can see that the centre of the circle ${x^2} + {y^2} = 9$ is $\left( {0,0} \right)$
From $\vartriangle OAB$,
$\Rightarrow \sin {45^0} = \dfrac{r}{{OA}}$ [$\therefore \sin \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotanuse}}}}$]
Using the distance formula, OA will be
$\Rightarrow OA = \sqrt {{{\left( {h - 0} \right)}^2} + {{\left( {k - 0} \right)}^2}}$
$\Rightarrow OA = \sqrt {{h^2} + {k^2}}$
So,
$\Rightarrow \sin {45^0} = \dfrac{r}{{\sqrt {{h^2} + {k^2}} }}$ [$\therefore \sin {45^0} = \dfrac{1}{{\sqrt 2 }},r = 3$]
$\Rightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{3}{{\sqrt {{h^2} + {k^2}} }}$
Cross-multiply on both sides,
$\Rightarrow \sqrt {{h^2} + {k^2}} = 3\sqrt 2$
Squaring both sides, we will get,
$\Rightarrow {h^2} + {k^2} = 18$
Replacing h by x and k by y,
$\Rightarrow {x^2} + {y^2} = 18$
Hence, this is the locus of intersection of two mutually perpendicular tangents.
Now, we have to find the equation of circle which touches this circle at point $\left( {\sqrt 2 ,4} \right)$

Let the equation of the required circle be
$\Rightarrow {x^2} + {y^2} + 2gx + 2fy + c = 0$ …… (ii)
The equation of tangent passing through $\left( {\sqrt 2 ,4} \right)$ be,
$\Rightarrow T = 0$
We know that,
Equation of tangent, T is given by
$\Rightarrow x{x_1} + y{y_1} + 2g\left( {\dfrac{{x + {x_1}}}{2}} \right) + 2f\left( {\dfrac{{y + {y_1}}}{2}} \right) + c = 0$
Here, we have $\left( {{x_1},{y_1}} \right) = \left( {\sqrt 2 ,4} \right)$
So, the equation of tangent, T will become
$\Rightarrow \sqrt 2 x + 4y + g\left( {x + \sqrt 2 } \right) + f\left( {y + 4} \right) + c = 0$
Separating x and y coefficients,
$\Rightarrow x\left( {\sqrt 2 + g} \right) + y\left( {4 + y} \right) + \sqrt 2 g + 4f + c = 0$ ……. (iii)
This is equation of tangent line.
Now, the equation of tangent line using the equation of circle ${x^2} + {y^2} = 18$ will be,
$\Rightarrow x{x_1} + y{y_1} - 18 = 0$
We have $\left( {{x_1},{y_1}} \right) = \left( {\sqrt 2 ,4} \right)$
So,
$\Rightarrow \sqrt 2 x + 4y - 18 = 0$ ……… (iv)
We know that, equation (iii) and equation (iv) both are the equation of tangent line,
So, the coefficients of both equations are proportional,
$\Rightarrow \dfrac{{g + \sqrt 2 }}{{\sqrt 2 }} = \dfrac{{f + 4}}{4} = \dfrac{{\sqrt 2 g + 4f + c}}{{ - 18}} = \lambda \left( {say} \right)$
Therefore,
$\Rightarrow g + \sqrt 2 = \sqrt 2 \lambda$
$\Rightarrow g = \sqrt 2 \left( {\lambda - 1} \right)$
And,
$\Rightarrow f + 4 = 4\lambda$
$\Rightarrow f = 4\left( {\lambda - 1} \right)$
And,
$\Rightarrow \sqrt 2 g + 4f + c = - 18\lambda$
$\Rightarrow c = - 18\lambda - \sqrt 2 g - 4f$
Putting the value of g and f, we will get
$\Rightarrow c = - 18\lambda - \sqrt 2 \left( {\sqrt 2 \left( {\lambda - 1} \right)} \right) - 4\left( {4\left( {\lambda - 1} \right)} \right)$
Solving this, we will get
$\Rightarrow c = - 18\lambda - 2\lambda + 2 - 16\lambda + 16$
$\Rightarrow c = - 36\lambda + 18$
We can write this as:
$\Rightarrow c = - 36\lambda + 36 - 18$
$\Rightarrow c = - 36\left( {\lambda - 1} \right) - 18$
Now, we will put these values of g, f and c in equation (ii)
$\Rightarrow {x^2} + {y^2} + 2gx + 2fy + c = 0$
$\Rightarrow {x^2} + {y^2} + 2\left( {\sqrt 2 \left( {\lambda - 1} \right)} \right)x + 2\left( {4\left( {\lambda - 1} \right)} \right)y - 36\left( {\lambda - 1} \right) - 18 = 0$
$\Rightarrow {x^2} + {y^2} - 18 + 2\sqrt 2 x\left( {\lambda - 1} \right) + 8y\left( {\lambda - 1} \right) - 36\left( {\lambda - 1} \right) = 0$
Taking common $2\left( {\lambda - 1} \right)$,
$\Rightarrow {x^2} + {y^2} - 18 + 2\left( {\lambda - 1} \right)\left[ {\sqrt 2 x + 4y - 18} \right] = 0$
As we know that, $\lambda$ is a constant so,
Let $2\left( {\lambda - 1} \right) = k$, where k is a constant.
$\Rightarrow {x^2} + {y^2} - 18 + k\left[ {\sqrt 2 x + 4y - 18} \right] = 0$
Hence, the equation of system of coaxial circles will be ${x^2} + {y^2} - 18 + k\left[ {\sqrt 2 x + 4y - 18} \right] = 0$

Note: Whenever we ask such types of questions, we have to remember that a coaxial system of circles is defined by the radical axis and any one of the circles. if c = 0, then the circles are all tangent to y axis and if c > 0, then the circles do not have common points and also if c < 1, then the circle will cut the radical axis.